[置顶] 泰晓 RISC-V 实验箱,配套 30+ 讲嵌入式 Linux 系统开发公开课
红黑树 IN Linux (一)
By Chen Jie of TinyLab.org 2016-09-01 21:07:25
前言:一杯茶,悠闲看代码
平平常常工作日,这个那个催着解问题;项目和产品时有新需求;或沟通妥协总算得结论;却又推导重新来 —— 使尽浑身解数,身在漩涡不由己。失落也许有,焦躁是常态,感觉身体被掏空。
终得喘一口气,忘却得失与进度,沏上一杯茶,享片刻悠闲,片刻宁静。再上一段优雅的代码,慢慢品,忽然明了,欣喜在心。

红黑树:定义
平衡二叉树中,根 到任一 叶 的路径一样长。由此搜任一节点,各分支的最坏情形恒定。然而插入或删除节点会破坏平衡,故需回复平衡。回复平衡较大代价使得 平衡二叉树 对插入和删除等“写操作”不喜。与之相对应的,红黑树中也是 根 到任一 叶的“路径长度”一样。此处“路径长度”,计颜色为“黑”的节点数。红黑树的“平衡”定义相对宽松,故而回复平衡代价相对小,对“写操作”也容悦。
红黑树活跃在许多软件中,比如需排序的场合(如著名的内存分配例程 jemalloc),或是需唯一性(如 std::map 的实现)。在「[jemalloc 之堆占用剖析·内部实现」文末,表达了 jemalloc 探索之旅远未完结。尤其核心数据结构 —— 红黑树尚未仔细领略。此文即为还愿,只不过本文参观的是 Linux 中的红黑树。
红黑树有 5 个约束条件:
| 序号 | 约束条件 | 图示 |
| 1 | 红黑树中的节点,非黑即红 | |
| 2 | 红黑树根节点为黑色 | |
| 4 | 红色节点,其子节点必为黑色 | |
| 3 | 所有叶子节点(null)都为黑色 | |
| 5 | 由根节点到各叶子节点,路径上的 黑色节点一样多 |
红黑树 IN Linux:特点
Linux 表示红黑树的基本结构体为 rb_node,如下图所示:
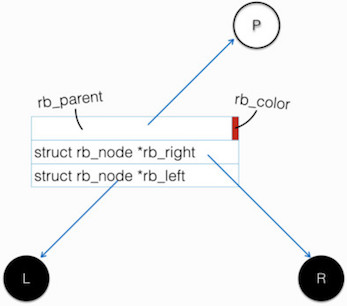
由上图可见,rb_node 中将“指向 父节点的指针”,与“本节点的 颜色”,合并到了一个名为 __rb_parent_color 的 long 型变量。出于性能考虑,对象内存地址确保 4 字节对齐(32位,即地址最低两位为 ‘0’),甚至是 8 字节对齐(64位,即地址最低三位为 ‘0’)。故可将颜色编码在地址末两位中,从而节省空间。
上图同时隐含假定了一个 “PL” 的系统,即 Pointer 和 Long 类型的长度一致,否则就不能把 父节点指针 塞到 long 型变量中了。
Linux 中的红黑树有额外两个特点:
- lockless lookup:即在允许牺牲部分准确性的前提下,无需持有锁,就能进行节点的检索操作。
- augment:augment 是补充的意思,即将每个节点,关联他处的某变量 —— 红黑树发生变化时,通过回调同步调整关联变量。
lockless lookup
来看一段来自 `____rb_erase_color()`、sibling 在左,Case 3 中的代码,这是一个以 sibling 为中心的树的左旋操作。注:源代码误将其注释为右旋操作。推测起来,大概是此处代码拷贝+修改自 “sibling 在右” 情形,但漏了改注释。开源第一定律 言 “足够多的眼睛,就可让所有问题浮现”,但即便如 Linux 这么成熟的项目,其不怎么吸引眼球的代码块,也隐藏一些或大或小的瑕疵。笔者对此的一个补丁在此:patchwork.kernel.org/patch/9302745
tmp1 = tmp2->rb_left; WRITE_ONCE(sibling->rb_right, tmp1); WRITE_ONCE(tmp2->rb_left, sibling); WRITE_ONCE(parent->rb_left, tmp2); | 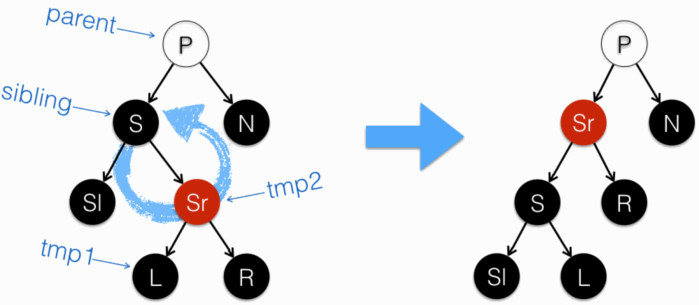 |
此处 WRITE_ONCE 是一个原子操作。在左旋操作中,tmp2(sibling 的右子)升为父节点,同时 sibling 本身降为 tmp2 的左子。注意其操作顺序:
- 把 tmp1(tmp2 的左子)过继给 sibling,做为其右子。tmp2 作为 sibling 原右子,暂时无父节点指向 —— 即从红黑树根节点开始,无法遍历到 tmp2。aka. tmp2 消失
- tmp2 收 sibling 作为左子,但其自身仍无父节点指向。aka. tmp2 仍然消失,但 tmp2 和 sibling 再次连接
- parent(原 sibling 的父节点),现指向了 tmp2。aka. tmp2 再次出现
这就是所谓的 lockless lookup 之代价 —— 牺牲部分准确性(tmp2 暂时不能被找到),但保证不出现 遍历有循环(比如先执行操作 2,就可能有 sibling –> tmp2 –> sibling)。lockless lockup 保证:搜寻某节点,若返回空,节点未必就不存在;但若返回非空,则返回结果是正确的。
另一处需留意的是,lockless lookup 目前仅关心 父节点指向子节点 的指针。对子节点的反向指针 __rb_parent_color 并不在意。
本节最后,让我们来看看 WRITE_ONCE 这个原子操作是如何实现的?
#define WRITE_ONCE(x, val) \
({ \
union { typeof(x) __val; char __c[1]; } __u = \
{ .__val = (__force typeof(x)) (val) }; \
__write_once_size(&(x), __u.__c, sizeof(x));\
__u.__val; \
}) | static __always_inline void __write_once_size(volatile void *p, void *res, int size)
{
switch (size) {
case 1: *(volatile __u8 *)p = *(__u8 *)res; break;
case 2: *(volatile __u16 *)p = *(__u16 *)res; break;
case 4: *(volatile __u32 *)p = *(__u32 *)res; break;
case 8: *(volatile __u64 *)p = *(__u64 *)res; break;
default:
barrier();
__builtin_memcpy((void *)p, (const void *)res, size);
barrier();
}
} |
左边是宏 WRITE_ONCE,右边是 WRITE_ONCE 中引用的内联函数 __write_once_size:
- WRITE_ONCE 是在地址 x 上写入值 val。保证“写入”是原子的。
__write_once_size是实际干活的函数,依据要 x 指向类型的长度,来决定写入方法:- 此处虽有
switch(size) ... case,但 size 在编译时刻就知晓(因为 x 是有类型的),且为内联函数,故实际生成汇编中不存在条件分支。 - 对于基本类型,直接赋值。其原子性由处理器指令,或编译器来保证。
- 注意
volatile在原子操作中出现。
- 注意
- 对于长度大于 64 字节的类型,“调用” 编译器内建 memcpy 函数。
- 此处虽说是“调用”,其实 gcc 会替换成一组指令来完成拷贝。
- 注意拷贝前后有内存屏障
barrier,确保 barrier 之后,对内存的更新到达“一致性的 cache 中(即总线上其他人可见)”。
- 此处虽有
- 再回到 WRITE_ONCE,它没有把 val 直接传给 __write_once_size,而是:
- 构造了一个 union。union 含有一个 char 类型成员
__c。 __write_once_size(&(x), __u.__c, ...,这么麻烦,没猜错的话是为了 Strict Aliasing。
- 构造了一个 union。union 含有一个 char 类型成员
augment
augment 是一个附加到 rb_node 上的外部变量,当红黑树发生变化(插入/删除节点)时,会通过下述回调,同步 augment:
struct rb_augment_callbacks {
void (*propagate)(struct rb_node *node, struct rb_node *stop);
void (*copy)(struct rb_node *old, struct rb_node *new);
void (*rotate)(struct rb_node *old, struct rb_node *new);
};
来看下 rb_augment_callbacks 是如何介入到插入节点(左边)和删除节点(右边)操作的:
// http://lxr.free-electrons.com/source/include/linux/rbtree_augmented.h?v=4.7#L57
static inline void
rb_insert_augmented(struct rb_node *node, struct rb_root *root,
const struct rb_augment_callbacks *augment)
{
__rb_insert_augmented(node, root, augment->rotate);
}
// http://lxr.free-electrons.com/source/lib/rbtree.c?v=4.7#L440
void __rb_insert_augmented(struct rb_node *node, struct rb_root *root,
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
__rb_insert(node, root, augment_rotate);
}
// http://lxr.free-electrons.com/source/lib/rbtree.c?v=4.7#L418
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
__rb_insert(node, root, dummy_rotate);
} | // http://lxr.free-electrons.com/source/include/linux/rbtree_augmented.h?v=4.7#L241
static __always_inline void
rb_erase_augmented(struct rb_node *node, struct rb_root *root,
const struct rb_augment_callbacks *augment)
{
struct rb_node *rebalance = __rb_erase_augmented(node, root, augment);
if (rebalance)
__rb_erase_color(rebalance, root, augment->rotate);
}
// http://lxr.free-electrons.com/source/lib/rbtree.c?v=4.7#L396
void __rb_erase_color(struct rb_node *parent, struct rb_root *root,
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
____rb_erase_color(parent, root, augment_rotate);
}
// http://lxr.free-electrons.com/source/lib/rbtree.c?v=4.7#L424
void rb_erase(struct rb_node *node, struct rb_root *root)
{
struct rb_node *rebalance;
rebalance = __rb_erase_augmented(node, root, &dummy_callbacks);
if (rebalance)
____rb_erase_color(rebalance, root, dummy_rotate);
} |
可以看到 插入的核心实现函数(__rb_insert)和 删除的核心实现函数(__rb_erase_augmented 和 ____rb_erase_color),都是接收 augment 相关回调作为参数。如不需要,传入 dummy_* 回调,由于是内联函数,dummy 的回调在编译时刻就被移除了。
要知道程序的某个特性,最好看它是怎么用的。下面我们从 struct vm_area_struct 中的红黑树,来看 augment 是如何使用的?
struct vm_area_struct {
/* The first cache line has the info for VMA tree walking. */
unsigned long vm_start; /* Our start address within vm_mm. */
unsigned long vm_end; /* The first byte after our end address
within vm_mm. */
/* linked list of VM areas per task, sorted by address */
struct vm_area_struct *vm_next, *vm_prev;
struct rb_node vm_rb;
/*
* Largest free memory gap in bytes to the left of this VMA.
* Either between this VMA and vma->vm_prev, or between one of the
* VMAs below us in the VMA rbtree and its ->vm_prev. This helps
* get_unmapped_area find a free area of the right size.
*/
unsigned long rb_subtree_gap;
...
vm_rb 是 vm_area_struct 链入红黑树的“插头”,rb_subtree_gap 就是附加到红黑树节点上的 augment。来看下本例中,rb_augment_callbacks 有哪些?
// http://lxr.free-electrons.com/source/mm/mmap.c?v=4.7#L371
RB_DECLARE_CALLBACKS(static, vma_gap_callbacks, struct vm_area_struct, vm_rb,
unsigned long, rb_subtree_gap, vma_compute_subtree_gap)
原来 rb_augment_callbacks 是通过宏 RB_DECLARE_CALLBACKS 来定义的。其中,传给宏的参数 rb_subtree_gap 指出了在 “内嵌 vm_rb 的结构体” 中,对应的 augment 是哪个成员;vma_compute_subtree_gap 则是个实实在在的函数。
以出镜率最高的 augment_rotate 回调为例,当进行过树旋转操作后,调用 augment_rotate,以原父节点作为第一个参数、新父节点作为第二个参数。可以看出新父节点继承了“老父节点的 augment”,而“老父节点的 augment” 则重新计算:
// http://lxr.free-electrons.com/source/include/linux/rbtree_augmented.h?v=4.7#L63
#define RB_DECLARE_CALLBACKS(rbstatic, rbname, rbstruct, rbfield, \
rbtype, rbaugmented, rbcompute) \
... \
static void \
rbname ## _rotate(struct rb_node *rb_old, struct rb_node *rb_new) \
{ \
rbstruct *old = rb_entry(rb_old, rbstruct, rbfield); \
rbstruct *new = rb_entry(rb_new, rbstruct, rbfield); \
new->rbaugmented = old->rbaugmented; \
old->rbaugmented = rbcompute(old); \
} \
rbstatic const struct rb_augment_callbacks rbname = { \
rbname ## _propagate, rbname ## _copy, rbname ## _rotate \
};
为了进一步理解,我们来看下 rb_subtree_gap 是什么?由上面代码,可以看出它是由 vma_compute_subtree_gap() 计算出来的:
static long vma_compute_subtree_gap(struct vm_area_struct *vma)
{
unsigned long max, subtree_gap;
max = vma->vm_start;
if (vma->vm_prev)
max -= vma->vm_prev->vm_end;
if (vma->vm_rb.rb_left) {
subtree_gap = rb_entry(vma->vm_rb.rb_left,
struct vm_area_struct, vm_rb)->rb_subtree_gap;
if (subtree_gap > max)
max = subtree_gap;
}
if (vma->vm_rb.rb_right) {
subtree_gap = rb_entry(vma->vm_rb.rb_right,
struct vm_area_struct, vm_rb)->rb_subtree_gap;
if (subtree_gap > max)
max = subtree_gap;
}
return max;
}
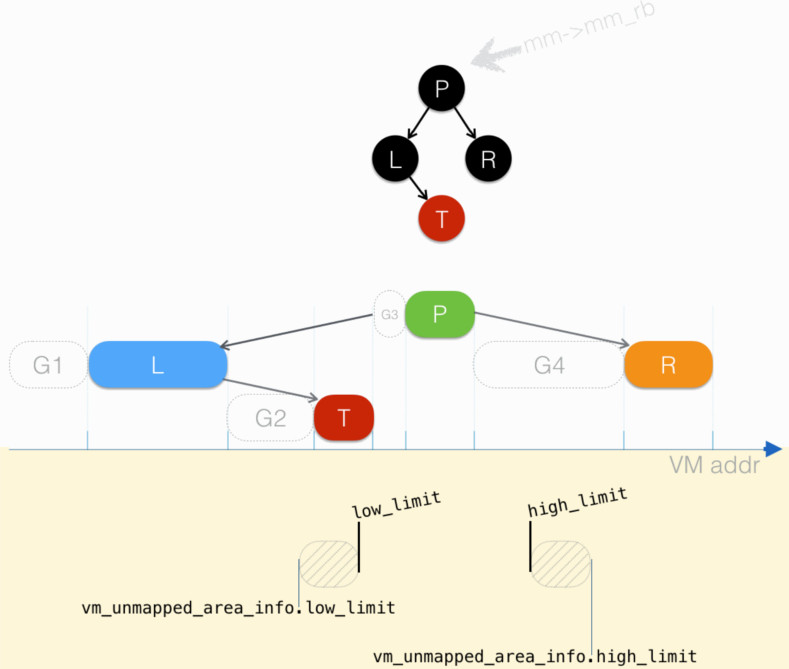
图例说明如下:图中上部为一个 vma 的红黑树,下部为 vma 在地址空间中的分布:
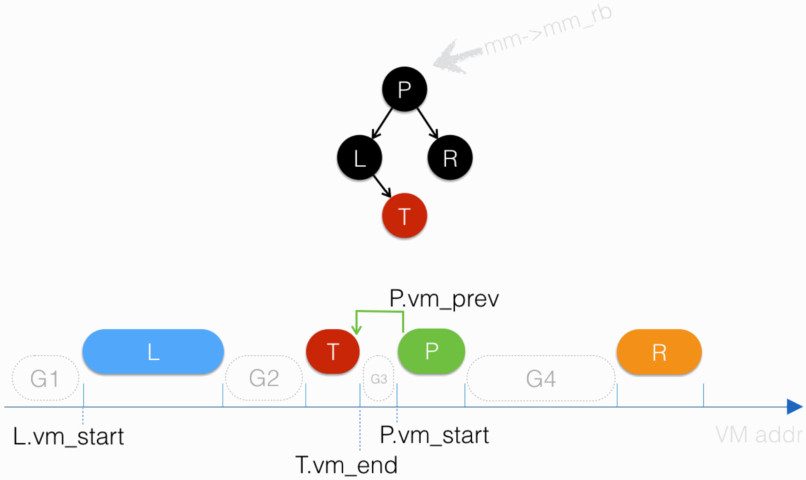
如果计算 P 这个节点的 rb_subtree_gap,则是以下弎值取最大:
- P.vm_start - T.vm_end
- L.rb_subtree_gap
- R.rb_subtree_gap
由于 rb_subtree_gap 由 vma_compute_subtree_gap() 计算得,单纯从计算角度看,vma_compute_subtree_gap() 是“递归”调己,这个“递归”在“叶子节点” T 和 R 处解套:
- T.rb_subtree_gap = T.vm_start - L.vm_end
- R.rb_subtree_gap = R.vm_start - P.vm_end
由此 L.rb_subtree_gap = max(L.vm_start, T.rb_subtree_gap)
图例中,G4 这个空隙最大,故 P.rb_subtree_gap = R.vm_start - P.vm_end,即为 紧贴着 P 名下节点的空隙中,最大空隙的尺寸。
要知道程序的某个特性,最好看它是怎么用的。下面从 unmapped_area() 来看 rb_subtree_gap 是如何发挥作用的?
下图配套说明 unmapped_area():
- 需要分配一个空间( 图中 斜虚线填充的圆角矩形 ),要求:
- 长度(
vm_unmapped_area_info.length,对齐到vm_unmapped_area_info.align_mask) - 从指定地址区间中分配(
vm_unmapped_area_info.high_limit,vm_unmapped_area_info.low_limit)
- 长度(
- unmapped_area() 试图找到满足要求的、地址最低 的空隙
- 若空隙都太小,且指定地址区间允许,则尝试从最高处(图中 R 之后的空间)分配
代入图例场景,这是个中序遍历(In-Order Traversal,即从低到高扫描)过程,其中 rb_subtree_gap 用来滤掉路径上 “名下空隙太小”的节点:
# 前提假定:待分配的空间,要么可在 P 名下空隙找到;要么没有符合要求的空闲空间
# 伪代码描述:找 P 名下满足分配要求、地址最低的空隙
#
# 出场变量简介:
# length: 分配请求的长度,对齐到`对齐要求'
# high_limit: vm_unmapped_area_info.high_limit - length
# low_limit: vm_unmapped_area_info.low_limit + length
#
# 要求:
# gap_start <= high_limit
# gap_end >= low_limit
# gap_end - gap_start >= length
# http://lxr.free-electrons.com/source/mm/mmap.c?v=4.7#L1621
gap_end = P.vm_start # i.e. G3.end
gap_end >= low_limit && P.rb_left && P.rb_left.rb_subtree_gap >= length?
# P.rb_left is L
# L.rb_subtree_gap = max(G1.size, G2.size)
# answer: yes, Try P.L
### Current is L !
gap_end = L.vm_start # i.e. G1.end
# L 没有左子节点
# check_current: http://lxr.free-electrons.com/source/mm/mmap.c?v=4.7#L1634
gap_start = 0 # i.e. G1.start
if (gap_start > high_limit) # 检查:gap_start 必小于等于 high_limit
return not found!!! # 不满足返回 not found !!! 这是因为剩余待查的空隙,其 gap_start 只会更大!
gap_end >= low_limit? # i.e. G1.end >= low_limit? answer: no
# Try P.L.T
# http://lxr.free-electrons.com/source/mm/mmap.c?v=4.7#L1641
### Current is T !
gap_end = T.vm_start # i.e. G2.end
# T 没有左子节点
# check_current
gap_start = L.end # i.e. G2.start
if (gap_start > high_limit)
return not found!!!
gap_end >= low_limit? # i.e. G2.end >= low_limit? answer: no
# T 没有右子节点
# 向上返回...直到返回 P 继续
# 对应代码:http://lxr.free-electrons.com/source/mm/mmap.c?v=4.7#L1652
### Current is P !
gap_start = T.vm_end # i.e. G3.start
gap_end = P.vm_start # i.e. G3.end
# check_current
if (gap_start > high_limit)
return not found!!!
gap_end >= low_limit? # answer: yes
gap_end - gap_start >= length? # i.e. G3.size > length? answer: no
# Try P.R
### Current is R !
gap_end = R.vm_start # i.e. G4.end
# R 没有左子节点
# check_current
gap_start = P.end # i.e. G4.start
if (gap_start > high_limit)
return not found!!!
gap_end >= low_limit? # answer: yes
gap_end - gap_start >= length? # i.e. G4.size > length? answer: yes
# found !!!
小结
本篇回顾了红黑树的 5 个约束条件,以及 Linux 中红黑树的额外两个特点。后续文章,我们将从插入和删除节点操作,来看红黑树经典算法在 Linux 中的实现。
猜你喜欢:
- 我要投稿:发表原创技术文章,收获福利、挚友与行业影响力
- 知识星球:独家 Linux 实战经验与技巧,订阅「Linux知识星球」
- 视频频道:泰晓学院,B 站,发布各类 Linux 视频课
- 开源小店:欢迎光临泰晓科技自营店,购物支持泰晓原创
- 技术交流:Linux 用户技术交流微信群,联系微信号:tinylab
| 支付宝打赏 ¥9.68元 | 微信打赏 ¥9.68元 | |
 |  请作者喝杯咖啡吧 |  |