红黑树 IN Linux （二）

By Chen Jie of TinyLab.org 2016-09-15 21:25:25

前言：

前文回顾了红黑树的 5 个属性，及 Linux 实现的红黑树所具备的额外俩属性：

1. lockless lookup
2. augment

lockless lookup 以部分准确性换取无需持锁查找。lookup 是指从根节点开始，一路向下，最终找到（或找不到）树中的一个位置（插言：这是个 “指位器 (iterator)” 的概念）。这要求 父节点指向子节点的指针 无需持锁访问；且更新过程中，不存在一刻指针成环。

augment 是附加在节点上的额外数据成员，并在树的增删操作中，同步更新此额外数据成员。 augment 可视作本节点、及子孙节点的“摘要”，比如在前文 unmapped_area() 例子中，augment（实际的数据成员叫做 rb_subtree_gap）记为 节点名下最大空隙的尺寸。于是，在分配 vma（遍寻 目标空隙）的过程中，能有效跳过 名下空隙均太小 的节点。

红黑树：删除一个节点

我们从一个函数调用栈入手：

// http://lxr.free-electrons.com/source/lib/rbtree.c?v=4.7#L424
void rb_erase(struct rb_node *node, struct rb_root *root)
{
	struct rb_node *rebalance;
	rebalance = __rb_erase_augmented(node, root, &dummy_callbacks);
	if (rebalance)
		____rb_erase_color(rebalance, root, dummy_rotate);
}

__rb_erase_augmented

此函数处理的情形，可分为两大类：

• 被移除的节点 N，最多只有一个子节点
• 被移除的节点 N，左右子节点都在

按照严格的定义，在 Linux 红黑树中叶子节点是 NULL。为方便期间，此处将 没有子节点（或说子节点都是 NULL）的节点称为“叶子节点”；只有一个子节点的（或说某个子节点是 NULL）的节点称为“半叶节点”。于是，第一大情形，实际上是删除 “（半）叶节点”：

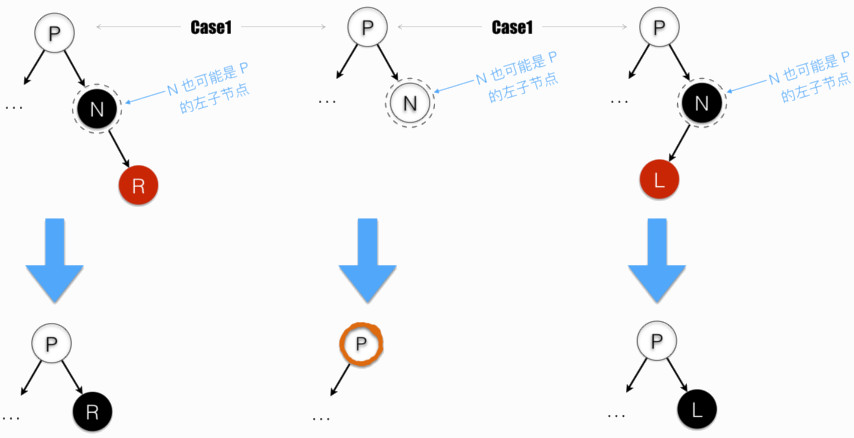
上图中，我们用 虚线圆 圈起被移除的节点 N。由于大前提假定 N 最多有一个子节点，若 N 有子节点，子节点必然为红色，此时 N 为黑色。这是由红黑树的属性 5，结合属性 4 所推结论。图中 没有着色的点，代表其颜色不确定，可能红，也可能黑。

图中左、右俩情形：N 被移除后，其唯一子节点继承了 N（继承内容：N 在红黑树中位置、以及 N 的颜色）。由于涉及路径上黑色节点数目未变，故红黑树保持平衡。无需做 rebalance。

图中中间情形：N 被直接移除。若 N 为红色，则涉及路径上黑色节点数目未变，红黑树平衡。反之若 N 为黑色，则失衡，需要 rebalance。此时最靠近叶的失衡节点 P，用 橙色墨迹 圈出。P 将传入 ____rb_erase_color 中，进行 rebalance。

再来看第二大情形，又可细分成俩情形 —— Case2 和 Case3：

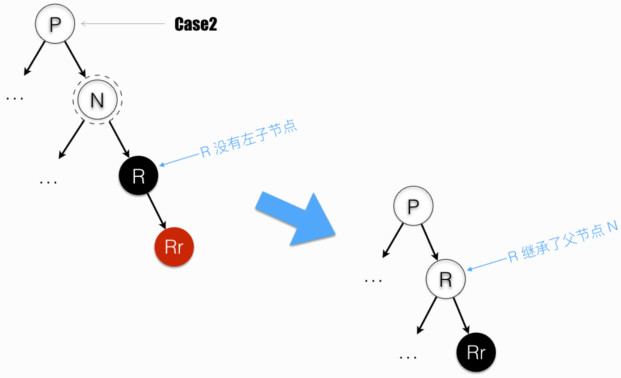
这是一个寻找 “N 的后继者” 的过程。红黑树是一个排序结构，“N 的后继者” 是指顺序上紧跟 N 的节点。即它右子节点名下，“最小”的节点。这个最小节点，有可能是右子节点本身（当右子节点没有左子时）即 Case2 所示情形；也可能是右子节点下，最靠左的节点，即 Case3 所示情形：

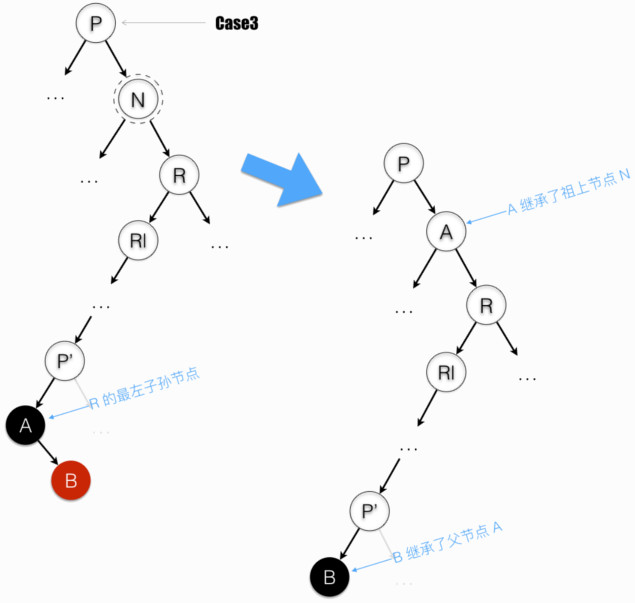
我们找到 “N 的后继者” 后，让它继承 N（继承内容：N 在红黑树中位置、以及 N 的颜色）。那么这个过程结束以后，需要 rebalance 吗？

—— 若 “N 的后继者” 还有子节点（如 Case2 和 Case3 的图例中的 Rr 和 B），让子节点 继承 “N 的后继者”（继承内容：位置、颜色），则保持涉及路径上黑色节点数不变，无需 rebalance。反之，则需从最靠近叶的失衡节点 R（Case2） 和 P’（Case3） 开始 rebalance。

____rb_erase_color

图例：如何达到平衡？

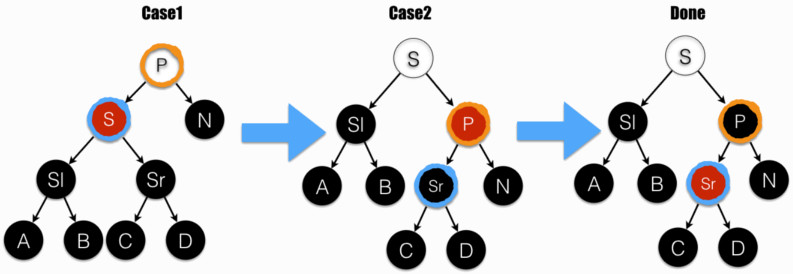
上图中，P 为最靠近叶的失衡点（橙色墨迹 圈出）；N 为 P 右子节点，其所在支路，比其兄弟节点 S（蓝色墨迹 圈出）所在支路，要/少一个黑色节点/。

图中从 Case1 到 Case2，在 P 上进行右旋操作：S 继承了 P 的颜色和位置，P 被设置成了红色。这就是函数 __rb_rotate_set_parents(P /* old */, S /* new */, root, RB_RED) 所做的工作。

然后交换 P 和 Sr 的颜色，P 的左右支变平衡。

上图中，密密排了许多节点，我们用右边的 N，抵消掉左边相应节点（A、B、C、D），从而让图示更加清爽：

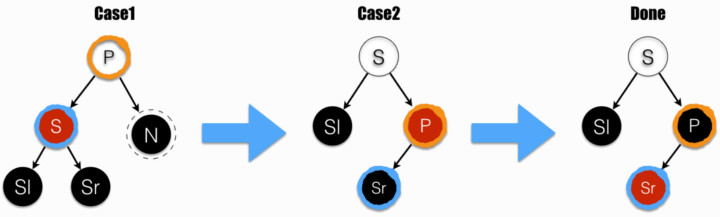
综上，我们看到树的旋转操作、置颜色之后，可达到平衡。

____rb_erase_color 骨架

// http://lxr.free-electrons.com/source/lib/rbtree.c?v=4.7#L223
____rb_erase_color(struct rb_node *parent, struct rb_root *root,
	...)
{
	struct rb_node *node = NULL, *sibling, *tmp1, *tmp2;
	 
	while (true) {
		sibling = parent->rb_right;
		if (node != sibling) {  /* node == parent->rb_left */
			...
		} else {   /* node == parent->rb_right */
			...
		}
	}
}

观察 __rb_erase_augmented 输出结果可知，若出现了失衡点（parent），则失衡点有且仅有一个子节点。该子节点即为 sibling（而 node 为 NULL）。

依据 sibling 在右（node == parent->rb_left），还是在左（node == parent->rb_right）分成两大块处理。两块的处理流程是对称的。

下面以 sibling 在左为例，阐述代码中的 Case1 - Case4。

Case1 和 Case2

一个隐含的条件为：/sibling 一支/ 比 /node 一支/ 多一个黑色节点。

• Case1：sibling （蓝色墨迹 圈出）为红色。
• Case2：sibling （蓝色墨迹 圈出）为黑色，且两子节点均为黑色（或不存在，即 NULL - 严格意义上的叶节点。按照红黑树属性 3 定义，叶节点都是黑色）。

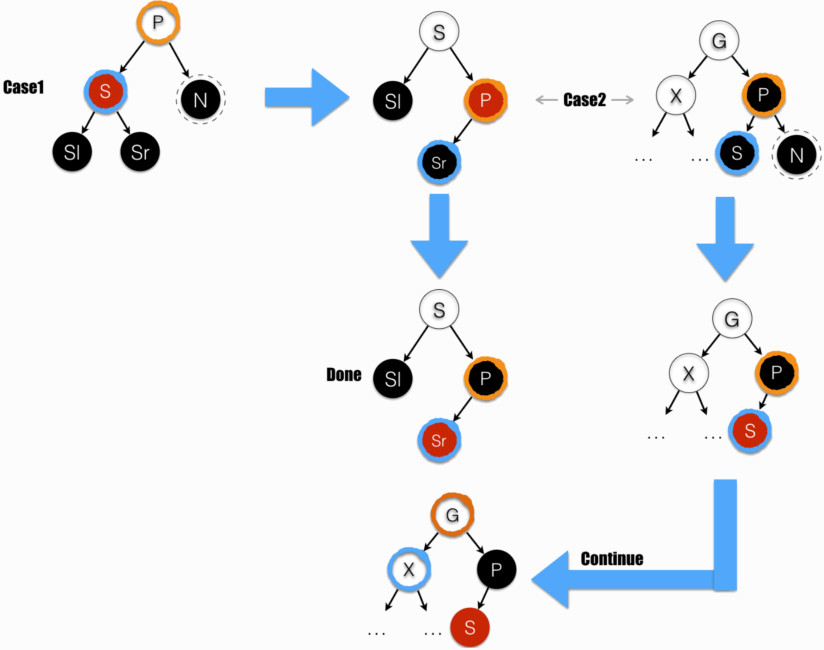
Case1 在 P 上进行了树的右旋操作，变化到了 Case2。

Case2 中对 parent（橙色墨迹 圈出）置黑色，sibiling（蓝色墨迹 圈出）置红色：

• 由于 Case2 中 sibling 置色前为黑色，故置红色使路径损失 1 个黑色节点，由此 parent 回复平衡。
• 但 grandparent 呢（即图中 G）？若 parent 置色前为红色，置色使路径增加 1 个黑色节点，刚好平衡。反之，G 成为最靠近叶的失衡节点，开始下一轮循环。
• 由 Case1 变化来的 Case2，parent 总是红色的，故能在本轮循环中达到平衡。

落在 Case1 和 Case2 的情形，要么本轮循环中达到平衡，要么进入下一轮循环。

Case3 和 Case4

一个隐含的条件为：/sibling 一支/ 比 /node 一支/ 多一个黑色节点。

• Case3：sibling（蓝色墨迹 圈出）为黑色；其左子节点为黑色（或不存在）； 其右子节点为红色。
• Case4：sibling（蓝色墨迹 圈出）为黑色；其左子节点为红色。
  • 注：由 Case3 变化而来的 “Case4”，并不符合上述描述 —— 特别是图例中，最靠近叶的失衡点为 Sr 而不是 P —— 这是个变化中的短暂特例，此处先忽略它。

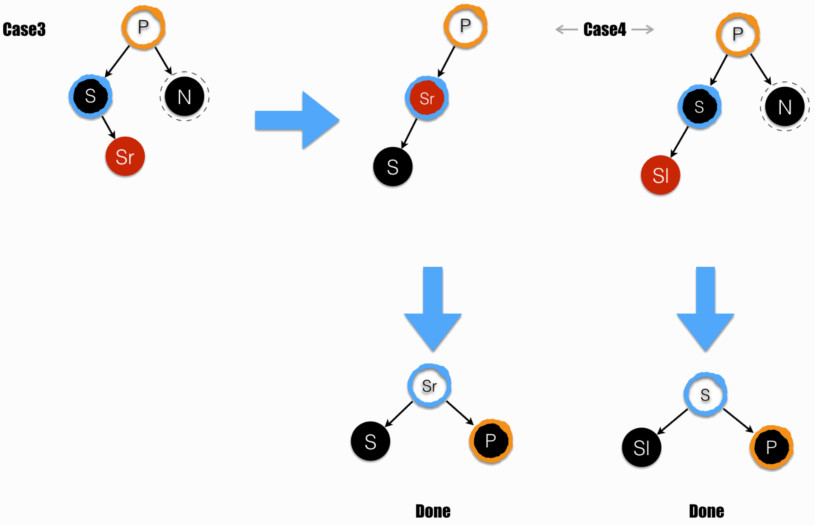
Case3 在 S 上进行了树的左旋操作，变化到了 Case4。

Case4 在 P 上进行了树的右旋操作：

• sibling 继承了 P（继承内容：位置和颜色）
• 右旋后，sibling 的左右子均置为黑色

落在 Case3 和 Case4 的情形，都能在本轮循环中达到平衡。

小结

本篇是「红黑树 IN Linux （一）」的续篇，前篇关注了 Linux 中红黑树的基础信息，本篇开始关注红黑树算法及其实现。我们从 删除和增加 节点操作入手，来一窥究竟。

限于篇幅，本文仅探讨了 删除 操作，对应 Linux 源代码中 __rb_erase_augmented 和 ____rb_erase_color 俩函数。

“删操作” 是相对较复杂的操作，下一篇我们将些许轻松地体验下 “增操作”。