泰晓科技 -- 聚焦 Linux - 追本溯源，见微知著！
网站地址：https://tinylab.org

泰晓RISC-V实验箱，转战RISC-V，开箱即用
请稍侯

IP 校验和计算优化：四两拨千斤

Chen Jie 创作于 2014/09/05
打赏

by Chen Jie of TinyLab.org 2014/09/05

前言

本文介绍一例龙芯(MIPS)上的 IP 校验和计算优化，来展示小调整带来大收益的一次优化体验。

首先来看优化结果：

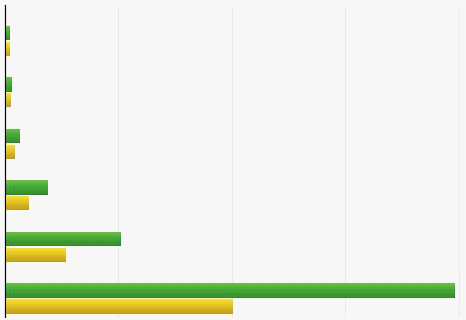
image

上图为 csum_partial 函数优化前后对比，自上而下分别为计算20字节、98字节、384字节、1440字节、4K字节和16K字节的时间开销，其中绿条为优化前，黄条为优化后。可以看到在 龙芯3A 处理器上，随着数据块的增大优化效果越明显，时间开销几乎减少一半。

阅读：IP校验和的实现

在 arch/mips/lib/csum_partial.S 优化实现了相关函数：

  • uint32_t csum_partial(const void *buffer, int len, uint32_t sum)

    对应 C 实现在 lib/checksum.c。计算当前 buffer 的校验和，结果并入传入的校验和（参数sum）。这是说我们可以将一个大 buffer，分片断来计算校验和。参数 len 必须是偶数，除非是最后一个片断。

  • uint32_t csum_partial_copy_from_user(const void __user *src, void *dst, int len, uint32_t sum, int *csum_err)

    对应C实现在 lib/checksum.c。该函数边拷贝，边计算校验和。其中拷贝的源地址可能位于用户空间，因此需要关照访存错误的情况（因此有返回参数 csum_err 来指明错误）。

    在MIPS实现中，该函数实际位于 arch/mips/include/asm/checksum.h，此处做了一个简单封装 —— 源地址在用户空间？__csum_partial_copy_from_user ：__csum_partial_copy_kernel —— csum_partial.S 优化了实际调用的后两函数。

我们知道RISC指令集访存方式为Load/Store，例如：

  • csum_partial 核心工作为:

    LOAD    temp, (src) # 装载到temp（某个寄存器）
ADDC(sum, temp)         # 结果保存到sum（某个寄存器）

  • csum_partial_copy* 核心工作为：

    LOAD    temp, (src)
ADDC(sum, temp)
STORE   temp, (dst) # 附带拷贝

  • ADDC 是个宏，展开成一组计算操作：

    #define ADDC(sum, temp1) \
ADD sum, temp1 \
sltu    temp2, sum, temp1 /* sum值是否比加数来的小，如是则溢出了(此时temp2被置1) */ \
ADD sum, temp2

优化这种大块数据的遍历处理，访存优化通常是关键。然而目测了一遍，发现当前代码已经高度优化了：

  • csum_partial 的优化实现，大体是按照逐级“升级”对齐条件的方法：

    Step1:   半字（16位）对齐 ? 下一个 : 升级到半字对齐（升级方法：处理一字节数据）

    Step2:   字（32位）对齐 ? 下一个 : 升级到字对齐（升级方法：处理半字数据）

    …

    一直到8字（256位，32字节）对齐，之后循环按块处理。（P.S. MIPS通用访存宽度为64位，即双字，为啥对齐条件要一直升到8字呢？一是方便替换成访存宽度更宽的指令，例如我们可以很方便地替换成龙芯128位访存指令gslq/gssq；另一方面大概是考虑缓存/数据预取的隐性对齐要求）

  • csum_partial_copy* 的优化实现

    抄/改自 memcpy 优化实现，即用左右部装载/存储指令，将目的地址（dst）升至64位对齐，然后依据源地址（src）对齐状况，两分支取一（左右部装载 vs 直接8字节装载）。

Tunning

尽管前述代码访存已经高度优化，我们还是骚包地用龙芯128位访存指令替换改造。令人意外的是性能不仅无提升，甚至有所退化。只能认为当前瓶颈不在访存上。

再来看数据处理这部分，也就是 ADDC 这个宏。大体上校验和计算是一个累加过程，但如果累加发生了溢出则给累加值加1，即：

sum = A + B >= UINT64_MAX+1 ? A+B-(UINT64_MAX+1)+1 : A+B

来想像一下一组 ADDC 计算：

ADDC(sum, A)
ADDC(sum, B)
ADDC(sum, C)
ADDC(sum, D)

每一次 ADDC 计算依赖前次计算结果（冠冕堂皇地说，这是个“真数据依赖”），因此是串行的。

为便于说明，简单介绍一下 CPU 的内部工作流程。把每条指令类比成一件要去衙门办的事。办事需要输入一堆材料，然后它给你处理下（例如梆梆梆盖几个章）出来一个输出材料。

现在开始工作了，想像一个办事窗口 —— 那是 CPU 的执行单元。然后你在排队，前面有一堆人。当你前面还有人时你不能出队，这叫做顺序执行（in-order）的结构。然而大部分高性能的 CPU 都是乱序（Out Of Order）执行的，因此重点来看乱序执行。

乱序执行中，在办事窗口（CPU执行单元，Execution Units）和排队的队伍间（重排队列，ReOrder Buffer ），有了一排等待叫号的座椅（保留站，Reservation Station）。

现在，轮到你出队，出了队直接坐到候号座位上，等着叫号，就是那种“请1225号客户到3号办事窗口…”。你被叫号的条件为：

  • 你办的这件事所需材料齐备
  • 并且办事窗口空闲

不然就得等待，大部分情况下你在等前面某个人的输出材料。这时，当此人的输出材料一产生（甚至他还没离开办事窗口），就 先行 送到你手上，同时通知你去办事窗口。

所谓乱序，是指等待叫号时，原来排在你后头的人可能会先于你去办事，比如他的输入材料已经齐了并且他要去的办事窗口空着。

当大家办完事以后，还是按原来顺序回到队伍中（故名重排队列）。然后一个一个按序退出办事大厅。

讲完了这个比喻，回头来看优化。首先访存指令之间、以及访存指令和 ADDC 可以无关，因此如下序列：

1   LOAD    A, (src)
2   LOAD    B, 8(src)
3   LOAD    C, 16(src)
4   LOAD    D, 24(src)
5   ADDC(sum, A)
6   ADDC(sum, B)
7   ADDC(sum, C)
8   ADDC(sum, D)

当 ’2′ 在访存窗口办事的时候，’5′ 可以在 ALU 窗口办事。当访存窗口办事效率很高的时候（因为有缓存，有预取），’6′ 就得傻等 ’5′ 的输出材料（sum值），’7′ 就得傻等 ’6′，’8′就得傻等’7′。想像一下，候号椅上坐满了人，而办事窗口多数空着，且每次只叫一个人去办事。那些排队的人看了捉急不？

如果可以…

1   ADDC(A, B)
2   ADDC(sum, A)
3   ADDC(C, D)
4   ADDC(sum, C)

这时 ’3′ 不用等 ’2′，两人可以同时去 ALU 窗口办事了（ALU 窗口可能不止一个，或者略等 ’2′ 进入 ALU 后走一个流水阶段）。

实际调整很少，详见补丁“MIPS: lib: csum_partial: more instruction parall”。

验证

在优化工作中，很重要的一个步骤是验证优化代码产生的结果与原先一致（对于某些优化，还可以是差异在误差允许范围内）。

那么如何验证前述指令调整前后是一致的呢？首先，我们在内核将对应函数实现变更为: 跑优化前函数 + 跑优化后函数 + 比较两次结果，差异则panic。跑了一段时间未见panic。

当然这不科学，最好作数学上的证明。

数学证明来了。为了便于表达，我们将：

  • ADDC(A, B)记为“A 烫 B”
  • 于是A **烫 B** = A + B >= @ ? A+B-@+1 : A+B
  • 64位无符号表达上限记为“@”，即@等于“2^64”
  • 对于参与运算的数A，其区间在[0, @-1]，即 uint64_t 所表示范围。

于是我们要证明“sum 烫 A 烫 B == sum 烫 (A 烫 B)”，这不就是证结合律嘛。

在“sum 烫 A 烫 B”中有两次加法，按照每次加法是否溢出，可以分成四种情况：

  • 加法1溢出，加法2不溢出。
  • 加法1不溢出，加法2溢出。
  • 加法1和加法2均溢出。
  • 加法1和加法2均不溢出。

情况1：加法1溢出，加法2不溢出

此时有：

1.1   sum + A >= @
1.2   sum + A - @ + 1 + B < @
sum 烫 A 烫 B = sum + A + B - @ + 1

假设A + B >= @

2   => A 烫 B = A + B - @ + 1

问 sum + (A 烫 B) = sum + A + B - @ + 1，溢出否？
=> sum 烫 (A 烫 B) = sum + A + B - @ + 1  # (1.2)

假设A + B < @

3   => A 烫 B = A + B

问 sum + (A 烫 B) = sum + A + B，溢出否？
4   sum + A + B >= @ + B >= @   # (1.1) 两边加B
=> sum 烫 (A 烫 B) = sum + A + B - @ + 1

情况2：加法1不溢出，加法2溢出

此时有：

1.1   sum + A < @
1.2   sum + A + B >= @
sum 烫 A 烫 B = sum + A + B - @ + 1

假设A + B >= @

2   => A 烫 B = A + B - @ + 1

问 sum + (A 烫 B) = sum + A + B - @ + 1，溢出否？
3   sum + A + B - @ + 1 < @ + B - @ + 1 # (1.1) 两边加B-@+1
4   => sum + A + B - @ + 1 < B + 1 <= @
5   => sum + A + B - @ + 1 < @
=> sum 烫 (A 烫 B) = sum + A + B - @ + 1

假设A + B < @

2   => A 烫 B = A + B

问 sum + (A 烫 B) = sum + A + B，溢出否？
=> sum 烫 (A 烫 B) = sum + A + B - @ + 1  #(1.2)

情况3：加法1和加法2均溢出

此时有：

1.1   sum + A >= @
1.2   sum + A + B - @ + 1 >= @
sum 烫 A 烫 B = sum + A + B - 2@ + 2

2   A + B >= 2@ - 1 - sum   # (1.2) 移项得
3   已知1 + sum <= @      # 0 <= sum <= @-1
4   => @ <= @ - 1 - sum + @
5   => @ <= 2@ - 1 - sum
6   => @ <= 2@ - 1 - sum <= A + B   # (2)
7   => A + B >= @       # (6) 整理得
8   => A 烫 B = A + B - @ + 1

问 sum + (A 烫 B) = sum + A + B - @ + 1，溢出否？
=> sum 烫 (A 烫 B) = sum + A + B - 2@ + 2 # (1.2)

情况4：加法1和加法2均不溢出

此时有：

1.1   sum + A < @
1.2   sum + A + B < @
sum 烫 A 烫 B = sum + A + B

2   A + B < @ - sum <= @    # (1.2) 移项得, sum >= 0
3   => A + B < @
4   => A 烫 B = A + B

问 sum + (A 烫 B) = sum + A + B，溢出否？
=> sum 烫 (A 烫 B) = sum + A + B  #(1.2)

小结：优化这件事

虽然本次优化仅做了较少改动，实际上却做了许多工作。

比如我们用龙芯128位访存指令来进一步优化访存。实际工作并不如所述那么轻松 —— 例如128位访存指令使用通用寄存器，却编码在协处理器2域。需要在内核态保持“协处理器2”处于使能状态。好在这些工作在memcpy/memset的龙芯优化时已经完成。

其次，优化是一个累积的过程。基于一个模型，拟定尝试的方向，逐一尝试，步步逼近。冲突时还需取舍。

最后，也是最重要的两点。

一是永远不要因为出发点是美好的，而漠视违背出发点的想法。通常我们会依据已有认知设计一个认为最优的原型，然后漠视不符合原型设计的做法。而实际上，那些例外有时就是突破。换一个意思就是要多做对比，多做尝试。

二是优化以后一定要验证正确性。据说程序员取得进展后，通常会过度自信，这种自信实则缺乏依据。这句话至少在我身上得到验证。所以还是要降低自己的“情态”，谨小慎微，仔细验证。


Read Related:

Read Latest: