[置顶] 泰晓 RISC-V 实验箱,配套 30+ 讲嵌入式 Linux 系统开发公开课
RISC-V CPU 设计(4): RISC-V CPU 设计理论分析与主要模块的实现
Corrector: TinyCorrect v0.1-rc3 - [comments tables images urls pangu autocorrect epw] Author: Fajie.WangNiXi YuHaoW1226@163.com Date: 2022/08/03 Revisor: Falcon falcon@tinylab.org Project: RISC-V Linux 内核剖析 Proposal: RISC-V CPU Design Sponsor: PLCT Lab, ISCAS
前言
CPU 作为计算机的核心部件,其设计过程总会给我们高深复杂的印象;但是,既然是计算机的电子元件,那么我们一定可以使用数字逻辑电路的相互组合得以实现。本文将分为两大部分:CPU 设计理论分析和 CPU 设计中主要模块的实现,让读者对于 CPU 设计不再陌生,并且也可以尝试利用 FPGA 设计出自己的 CPU。
CPU 设计理论分析
CPU 的功能,用一句话来说就是要去执行指令。那么首先,我们将从 CPU 执行指令的过程开始讨论,并在讨论中逐步延伸以探究指令执行所需的必要操作,最后从数据通路的角度引导我们思考对实现各个操作模块的设计。
CPU 执行指令的过程
对于 CPU 而言,其功能就在于执行指令,本节将对指令执行的过程进行分析。
CPU 指令执行的大框架如下:
在流程图中,我们可以将各个操作分类到不同的指令执行阶段,以便于 CPU 设计过程中对各操作进行分析:
- 取指令阶段:
- 取指令
- PC+1 送至 PC
- 译码和执行阶段:
- 指令译码
- 内存地址计算
- 取操作数
- 算术逻辑运算
- 存储结果
- 自陷处理阶段:
- 判断和检测异常事件、异常处理
- 判断和检测中断事件、中断处理
指令执行所需的必要操作
在了解指令执行过程并进行相应分类后,我们可以根据分类和 RISC-V 指令集架构的要求对指令所必须完成的操作进行分析。在这里,就会体现出 RISC-V 作为精简指令集的优势:指令长度固定,指令类型数量固定。
通过 本系列第一篇文章 的介绍,我们可以很清楚的看到在 RISC-V 中,每条指令的功能总是由以下 4 种基本操作来实现:
- 读取某一内存单元的内容,并将其装入某个寄存器
- 将一个数据从某个寄存器中取出,并存储到给定地址的内存单元中
- 将一个数据从某个寄存器中取出,并送入另一个寄存器,或送入 ALU(算术逻辑单元)中
- 进行某种算术运算或逻辑运算,并将结果送入某个寄存器中
将操作分类后,我们便可以对数据通路进行讨论,在数据通路中分析各个模块并定义每个模块需要实现的功能。
数据通路
数据通路的位置
我们知道在冯诺伊曼体系中,计算机是由五大部件组成:运算器、控制器、存储器、输入设备、输出设备。那么在此结构中 CPU 充当的就是运算器和控制器的角色,可以用下图来表示:
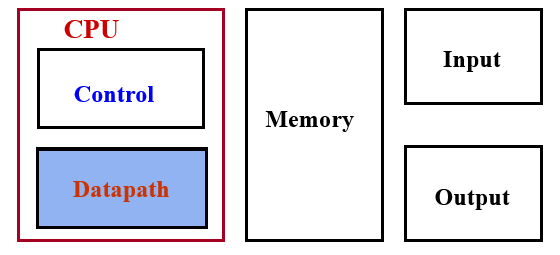
从图中可以看到,我们将运算器进一步具体化,成为了数据通路。所以,数据通路就是在指令执行过程中,数据所经过的路径,包括路径中的部件。所以数据通路是指令的执行部件,刚好对应了运算器的功能。
同时图中也清楚的表示,CPU 还需要具备控制器的功能,即对指令进行译码,生成指令对应的控制信号,控制数据通路中的各个动作,能对执行部件发出控制信号。所以控制器是指令的控制部件。
数据通路的基本结构
数据通路,其本质是一个数字逻辑电路。所以数据通路需要由两类部件组成:
- 组合逻辑元件(在 CPU 中也称为操作元件)
- 存储元件(在 CPU 中也称为状态元件)
而对于精简指令集,将元件之间连接的最好方式就是模块化分散连接,即将各元件模块化设计后相互连接构成数据通路。
数据通路中的时序控制
在数据通路中,由于同时存在组合逻辑电路和时序逻辑电路,所以需要使用同步系统对时序进行控制,同步系统的要求如下:
- 所有动作都有专门的时序信号来定时
- 由时序信号规定何时发出什么动作
例如:指令执行过程每一步都有控制信号控制,由定时信号确定控制信号何时发出、作用时间多长
在早期的计算机中,曾使用过三级时序系统:机器周期 => 节拍 => 脉冲。但现代计算机由于晶振技术和电子技术的提升,已不再采用三级时序系统,故整个数据通路中的定时信号就是时钟。我们知道数据通路的本质是组合逻辑电路和时序逻辑电路,而两者的基本单元又分别是操作元件和状态元件,所以数据通路的电路结构就十分清晰,是由状态元件和操作元件交替连接而构成的,如下图所示:
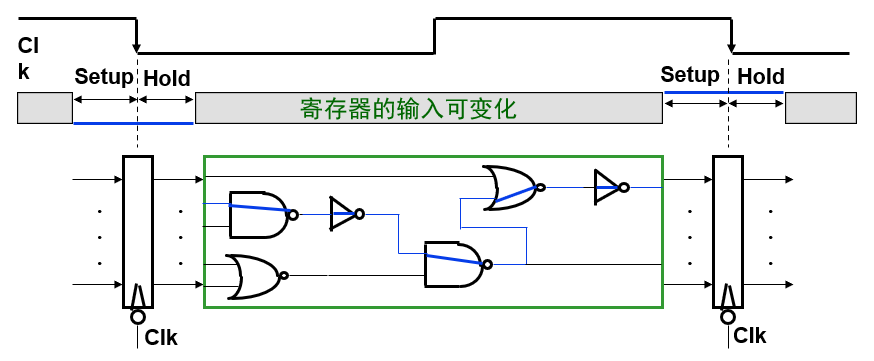
在数据通路中,只有状态元件能存储信息,所有的操作元件都必须从上一层的状态元件的输出获得数据,作为自己的输入;同时操作元件的输出又将向后写入下一层的状态元件,作为状态元件的输入。假定在数据通路采用下降沿触发的时钟信号进行时序控制,则会有以下结论:
- 所有状态元件在下降沿写入信息,经过一个 Latch Prop 锁存延迟(本小节中涉及到的数字逻辑电路知识,可参考 本系列的数电基础知识文章 进行了解)后输出保持有效
- 时钟周期时间 = 锁存延迟 + 最长延迟路径(电路硬件决定)+ 建立时间 + 时钟最大偏移(晶振决定)
CPU 中主要模块的实现
由上一小节分析,我们可以知道想要搭建出一条完整的数据通路,首要的就是设计出构成数据通路的两大基本元件:操作元件和状态元件。本节将对 CPU 中主要元件进行设计层面的分析,并使用 SpinalHDL 框架和 Verilator 来实现与仿真测试。
操作元件是组合逻辑电路的基本单元,在 CPU 中主要的模块是:
- 加法器(Adder)
- 多路选择器(MUX)
- 算术逻辑部件(ALU)
- 译码器(Decoder)
在数字逻辑电路文章中已经对多路选择器和译码器进行过讲解,这里不再赘述。下面将先从加法器的实现原理开始,逐步深入最后利用 SpinalHDL 实现一个 64 位宽的加法器。
加法器 Adder
整数加减运算
首先,我们从数学角度来介绍计算机中整数加减运算的原理。
在计算机的存储中,存在两种整数的存储形式:二进制编码和补码,分别用来表示无符号整数和带符号整数。下面简单讲解两者的区别:
- 二进制编码
- 其本质为纯数学上的二进制数,每一位代表 2 的幂次。举例来说,一个 64 位宽数值的二进制编码为 $b_{63}b_{62}b_{61}…b_2b_1b_0$(其中 $b_i\in \lbrace0,1\rbrace$),则其对应十进制整数就是 $b_{63}\cdot 2^{63}+b_{62}\cdot 2^{62}+b_{61}\cdot 2^{61}+…+b_2\cdot 2^2+b_1\cdot 2^1+b0\cdot 2^0$
- 补码
- 补码出现的目的是为了表示带符号的整数,所以我们知道其最高位 MSB 是作为符号位使用的:MSB 为 0 时表示正数,MSB 为 1 时表示负数。而在计算机中,想要计算出补码所对应的带符号整数值,就需要引入数学上的负权概念。
- 在补码中,最高位 MSB 由于起到了符号位的作用,且 MSB 为 1 时表示负数,我们便可以将 MSB 表示为负权,即其对应的 2 的幂次为负数,从而实现对补码计算出其真实值的功能。
- 举例来说,一个 64 位宽的补码为 $b_{63}b_{62}b_{61}…b_2b_1b_0$(其中 $b_i\in \lbrace0,1\rbrace$),则其对应的十进制整数就是 $-b_{63}\cdot 2^{63}+b_{62}\cdot 2^{62}+b_{61}\cdot 2^{61}+…+b_2\cdot 2^2+b_1\cdot 2^1+b0\cdot 2^0$
对于 RV64I 指令集而言,其规定有 add、addu、sub、subu 共 4 种基本运算指令。而利用数学上二进制编码和补码的运算规则,我们便可以实现一个加法器了。
整数加减运算规则
- 二进制编码
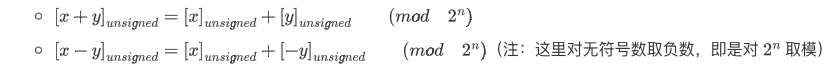
- 补码
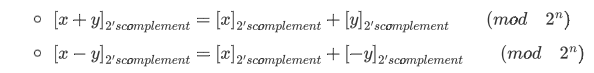
在加法上,二进制编码和补码没有差异;而在减法上,虽然二者形式上没有差异,但我们必须确认两者在数学上完全相等才能得出加法器的普适性结论。
对于二进制编码取负,本质是对 $2^n$ 取模;而对于补码取负数,则相当于其最高位由负权变成了正权(此时已经转化为和无符号二进制编码一样的形式了),那么再对 $2^n$ 取模时:
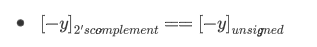
所以,此时可以得到结论:加法器可适用于所有二进制编码和补码的加减法。
加法器的实现
有了以上讨论的数学基础,我们便可以用示意图展示一个加法器的结构了:
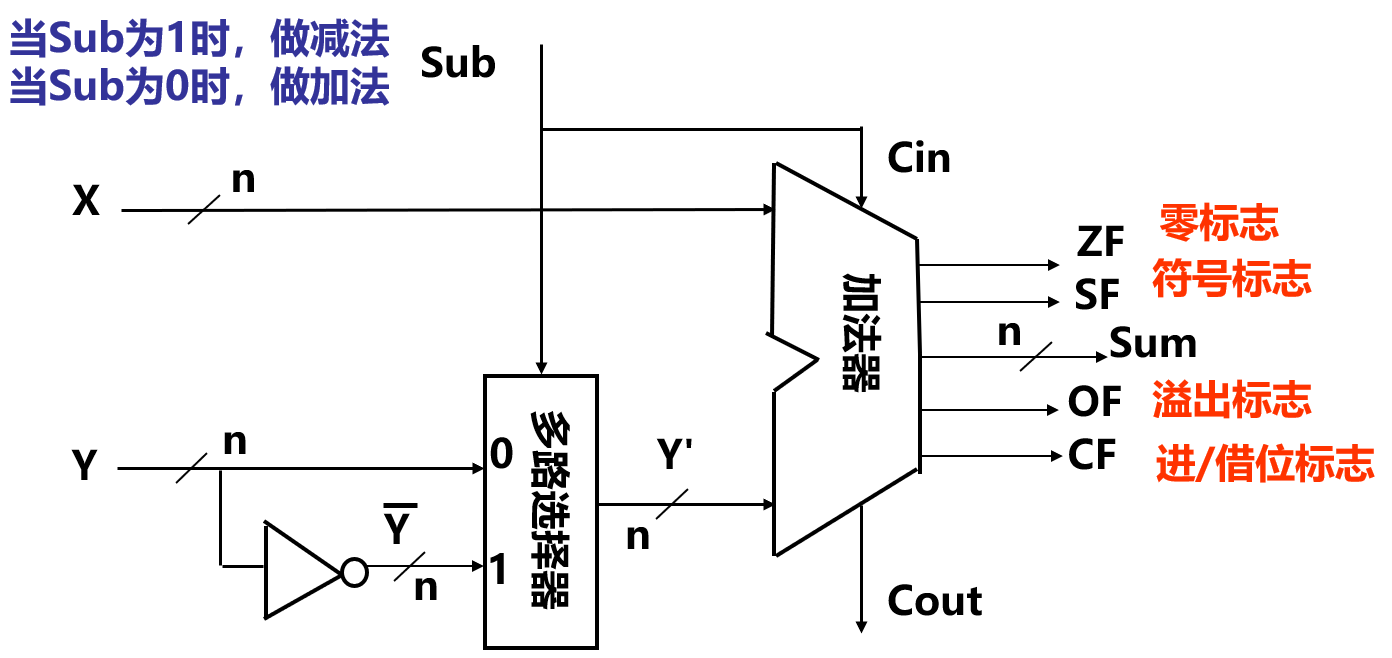
在图中我们可以看到,对于加法器而言,并不存在加法或是减法的区分,在硬件上加法器只做加法。那么由上面的数学表示,减法是通过对数字取负,而在计算机中,实质上就是取反加一的动作。
为了数据通路中后续操作的控制信号,加法器必须给出以下 4 个条件标志:
- $ZF$:Zero Flag 零标志,表示加法器得到的结果为 0
- $SF$:Sign Flag 符号位标志,表示加法器得到结果中的最高位
- $OF$:Overflow Flag 溢出标志,表示加法器做完运算后结果溢出
- $CF$:CarryOut Flag 进位/借位标志,表示加法器做完运算后是否存在进位或借位的情况
下面对各个条件标志给出逻辑运算公式:
- $ZF = 1$,当且仅当 Sum = 0
- $SF = Sum_{n-1}$
- $CF=Cout\bigoplus Sub$
- $OF$ 的计算公式较为复杂,其本质是判断两个正数或两个负数相加时是否会溢出,公式如下:
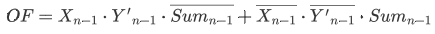
我们可以通过两个例子来理解加减法的原理:
- 加法实例
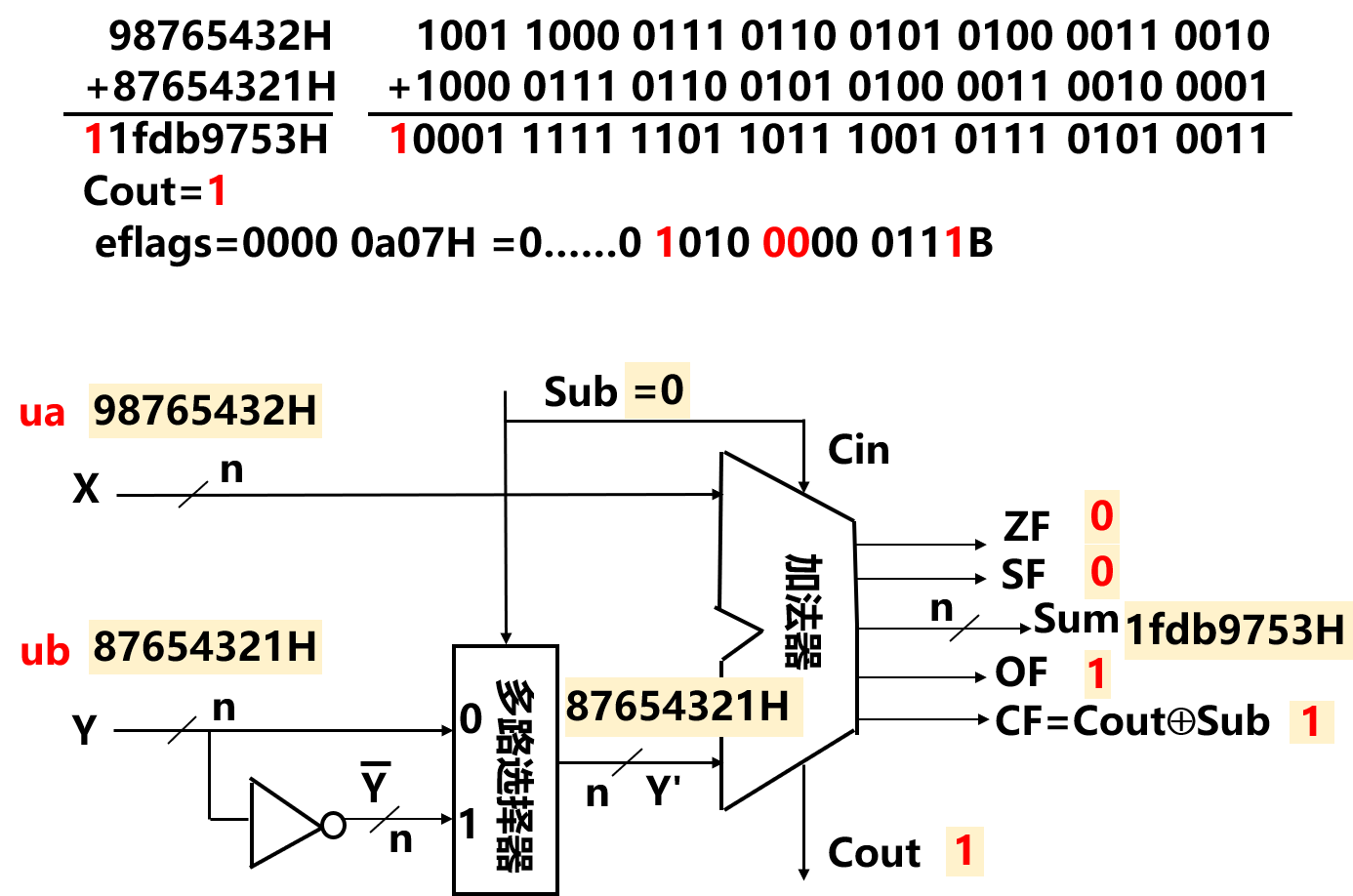
- 减法实例
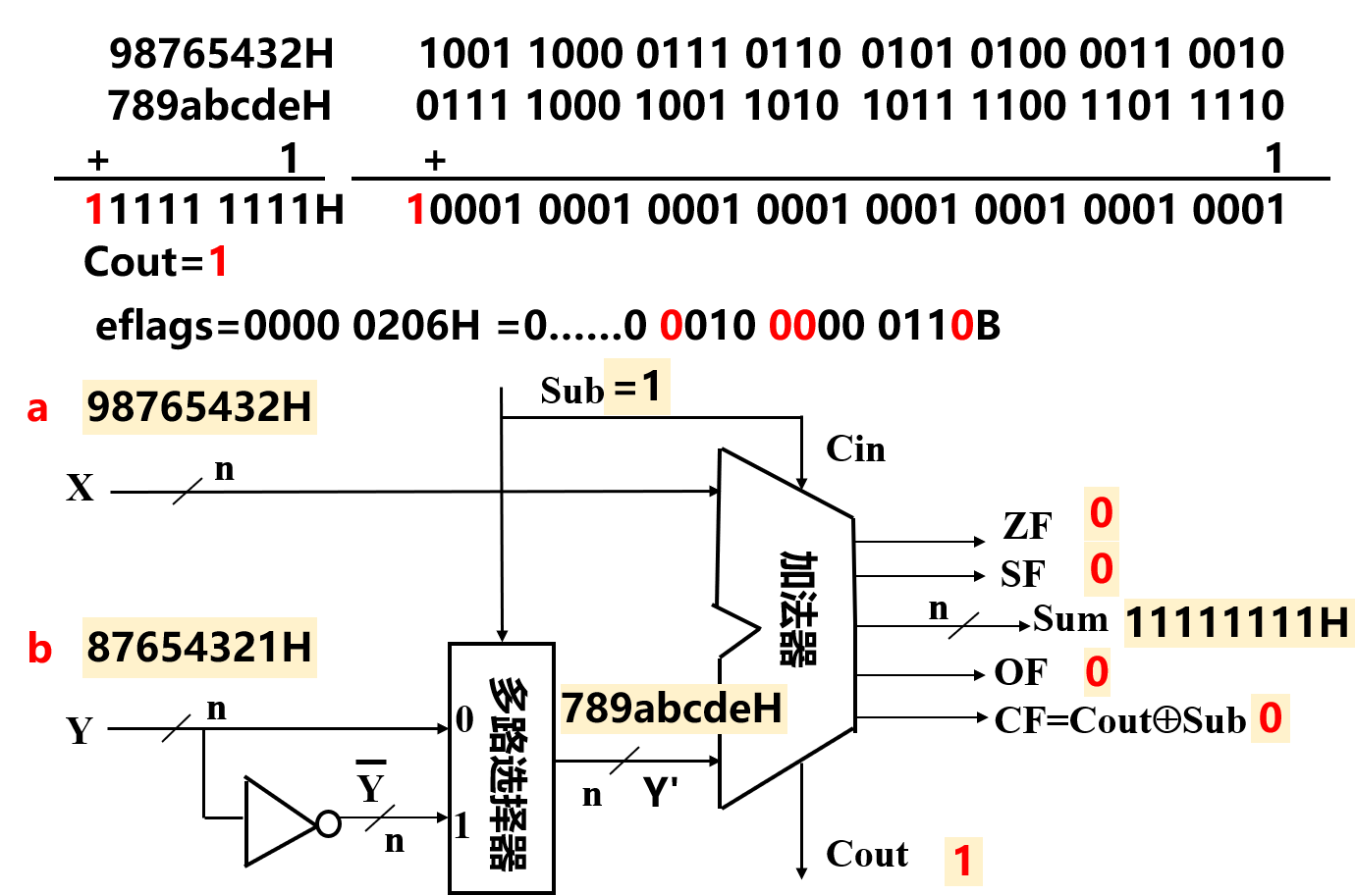
SpinalHDL 的实现
在具备了以上前置知识以后,我们就可以使用 SpinalHDL 框架实现加法器:
package alu
import spinal.core._
import spinal.lib._
class Adder extends Component {
val io = new Bundle {
val data1 = in UInt (64 bits)
val data2 = in UInt (64 bits)
val subCtr = in Bool()
val carryOut = out Bool()
val overflow = out Bool()
val sign = out Bool()
val zero = out Bool()
val adderResult = out UInt (64 bits)
}
noIoPrefix()
val tempResult = UInt(65 bits) //one more bit for carry out
//CAUTION: Here we need to use +^ as add with carry
when(io.subCtr) {
tempResult := io.data1 +^ io.data2 + 1
} otherwise {
tempResult := io.data1 +^ io.data2
}
when(tempResult === 0) {
io.zero := True
} otherwise {
io.zero := False
}
// Only when data1 and data2 are same sign while tempResult has a reversed 'sign bit', overflow happens
io.overflow := (io.data1.msb & io.data2.msb & ~tempResult(63)) | (~io.data1.msb & ~io.data2.msb & tempResult(63))
io.sign := tempResult(63)
io.carryOut := tempResult.msb
io.adderResult := tempResult(63 downto 0)
}
object AdderVerilog {
def main(args: Array[String]): Unit =
SpinalConfig(
mode = Verilog,
targetDirectory = "verilog/ALU"
).generate(new Adder)
}
算术逻辑单元 ALU
在 ALU 中,我们需要完成 4 个子模块的设计,分别是:
- 加法器(完成算术加减运算,对应
add、addi、addu、sub、subi、subu指令) - 移位器(完成移位运算,对应
sll、slli、srl、srli、sra、srai指令) - 逻辑运算器(完成逻辑运算,对应
and、andi、or、ori、xor、xori指令) - 比较器(完成比较运算,对应
slt、sltu、slti、sltiu指令)
所以我们可以首先画出一个基本的 ALU 框架图来划分出各个功能子模块:
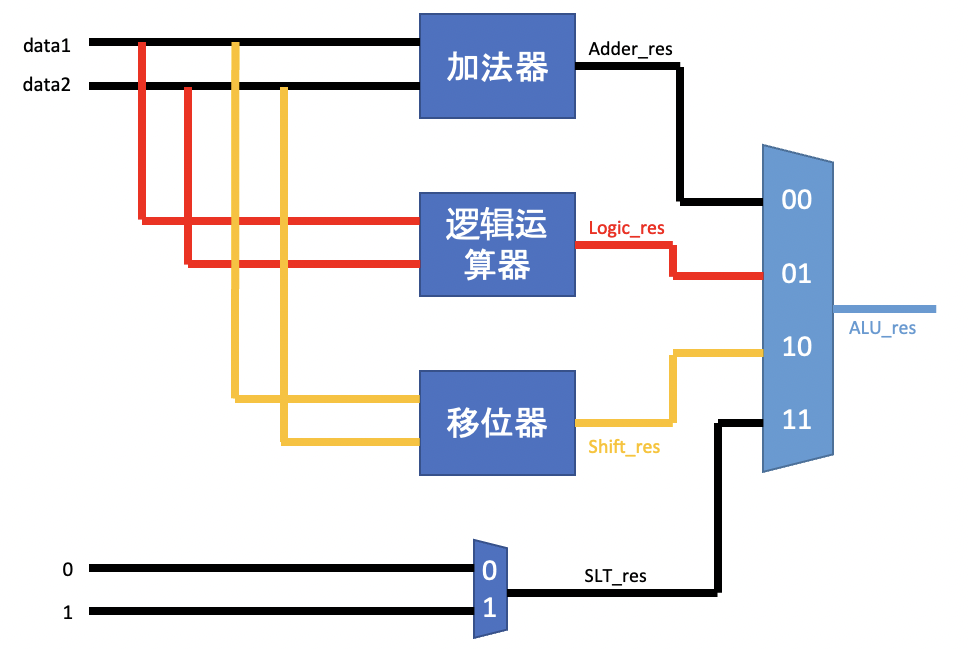
下面我们将对各个模块进行设计方面的介绍:
利用 SpinalHDL 的便捷特性,我们可以通过基本数据类型的转换实现算术和逻辑移位的操作,从而实现移位器模块。
首先考虑控制信号的设计,移位器的主要任务共有三条:
- 逻辑右移(即高位补 0)
- 算术右移(即高位补符号位)
- 左移
显然,3 个选项需要有 2 位宽的控制信号进行筛选。设定控制信号变量名为 shiftCtr,则对应三个选项可以做出如下的设计:
- 00 => 左移
- 01 => 算术右移
- 10 => 逻辑右移
接着考虑如何实现移位
- 左移:我们可以在这里运用一个小技巧:使用右移来获取左移结果,这是一种面向面积优化的电路设计,好处是减少使用 3 个独立的移位运算符来实现移位器(每个独立的移位器本质上是对 64 个 64 位宽的数据进行 64 选 1 的操作,会导致整体逻辑的面积大、延迟长)。根据
shiftCtr控制信号的值,当发出左移信号时,我们可以利用 SpinalHDL 中 UInt 数据类型的reversed属性直接获取高低位反转的 UInt 变量,此时进行右移后再利用reversed属性就可以直接获取到左移的值 - 算术右移:由于算术右移需要保持符号位不变,所以我们可以使用掩码的方式,在掩码中将需要填补的符号位所在的下标置位并同一个 64 位宽的全部由原数据符号位组成的数值进行与运算,最后在或运算上逻辑右移的值,就可以直接得到算术右移的值了
- 逻辑右移:由于一开始我们就采取了利用右移获取左移数据的方式,而本身 UInt 数据类型的右移操作默认即是逻辑右移,所以可以直接获得到结果
最后,我们可以根据上述理论设计在 SpinalHDL 框架下对移位器进行实现:
package alu
import spinal.core._
import spinal.lib._
class Shifter extends Component {
val io = new Bundle {
val data = in UInt (64 bits)
val shamt = in UInt (5 bits)
val shiftCtr = in UInt (2 bits)
val shiftResult = out UInt (64 bits)
}
noIoPrefix()
/*
shiftCtr =
00 left shift
01 arithmetical right shift
10 logical right shift
*/
val tempShift = UInt(64 bits)
//trick: use right shift to get left shift
tempShift := ((io.shiftCtr === 0) ? io.data.reversed | io.data) |>> io.shamt
val leftShiftResult = UInt(64 bits)
leftShiftResult := tempShift.reversed
val arithRightShiftResult = UInt(64 bits)
val sraMask = UInt(64 bits)
sraMask := ~(U"64'hffff_ffff_ffff_ffff" |>> io.shamt)
arithRightShiftResult := tempShift | (sraMask & U((63 downto 0) -> io.data.msb))
val logicRightShiftResult = tempShift
io.shiftResult := io.shiftCtr.mux(
0 -> leftShiftResult,
1 -> arithRightShiftResult,
2 -> logicRightShiftResult,
default -> U"64'b0"
)
}
object ShifterVerilog {
def main(args: Array[String]): Unit = {
SpinalConfig(
mode = Verilog,
targetDirectory = "verilog/ALU"
).generate(new Shifter)
}
}
下面的逻辑运算模块,可以直接利用 SpinalHDL 中的逻辑运算符完成,故可以不设计单独的模块。但是我们仍需要考虑控制信号的问题,在逻辑运算模块中,我们需要完成的任务有 3 个:
- 与运算
- 或运算
- 异或运算
所以同理,控制信号需要有 2 位宽。设变量名为 logicCtr,则对应三个选项可以做出如下的设计:
- 00 => 与运算
- 01 => 或运算
- 10 => 异或运算
所以,在 SpinalHDL 中我们可以设计出如下的代码:
// Logical calculator
val andResult = io.data1 & io.data2
val orResult = io.data1 | io.data2
val xorResult = io.data1 ^ io.data2
val logicResult = logicCtr.mux(
0 -> andResult,
1 -> orResult,
2 -> xorResult,
default -> S"64'b0"
)
最后的比较器模块,需要加法器的帮助,所以其本质上需要使用加法器做减法后发出的条件标志来对两数大小进行比较:
- 对于
slt和slti指令,两者都比较带符号整数,所以评判大小的标准则是加法器发出的 $SF$ 以及 $OF$ 标志:- 当 $SF \bigoplus OF == 1$ 时,表示 data1 小于 data2,结果应当为 1
- 当 $SF \bigoplus OF == 0$ 时,表示 data1 大于 data2,结果应当为 0
- 对于
sltu和sltiu指令,两者比较的是无符号整数,所以评判大小的标准应当是加法器发出的 $CF$ 标志:- 当 $CF==0$ 时,表示 data1 大于 data2,结果应当为 0
- 当 $CF==1$ 时,表示 data1 小于 data2,结果应当为 1
所以,在 SpinalHDL 中我们进行如下的设计:
// for SLT & SLTU
val sltLess = adderSign ^ adderOverflow
val sltuLess = ~adderCarryOut
val sltResult = (signCtr ? sltLess | sltuLess) ? S"64'b1" | S"64'b0"
至此,各模块设计完毕。下面要对 ALU 这一大模块中的控制信号进行设计,根据 RV64I 指令集以及数据通路的分析,我们可以知道 ALU 作为核心的运算器需要能够实现以下功能:
- 加法器
- 整数加法(包括无符号整数和带符号整数)
- 整数减法(包括无符号整数和带符号整数)
- 整数比较
- 无符号整数比较
- 逻辑运算模块
- 与运算
- 或运算
- 异或运算
- 移位器
- 左移
- 逻辑右移
- 算术右移
共有 10 个功能,故至少需要 4 位宽的控制信号对其进行功能的筛选。同时由于 ALU 的输出结果是在 4 个结果(加法器结果、移位器结果、逻辑运算结果、比较器结果)中进行筛选的,此处至少还需要 2 位宽的控制信号对各个子模块的结果进行筛选来获取 ALU 模块的最终结果。
设 2 位宽的结果筛选控制信号为 opCtr,我们可以自行设计对应关系:
- 00 => 加法器
- 01 => 比较器
- 10 => 移位器
- 11 => 逻辑运算器
对于 4 位宽的功能筛选控制信号,设为 aluCtr,由于还需要根据此信号生成各个子模块的控制信号,我们可以通过列表的方式来设计:
| aluCtr | signCtr | subCtr | ovCtr | shiftCtr | logicCtr | |
|---|---|---|---|---|---|---|
| ADD | 0000 | 1 | 0 | 1 | - | - |
| SLT | 0001 | 1 | 1 | 1 | - | - |
| SLTU | 0010 | 0 | 1 | 0 | - | - |
| AND | 0011 | - | - | - | - | 00 |
| OR | 0100 | - | - | - | - | 01 |
| XOR | 0101 | - | - | - | - | 10 |
| SLL | 0110 | - | - | - | 00 | - |
| SRL | 0111 | - | - | - | 10 | - |
| SUB | 1000 | 1 | 1 | 1 | - | - |
| SRA | 1001 | - | - | - | 01 | - |
所以,我们现在就可以根据上表画出带控制信号的 ALU 图示:
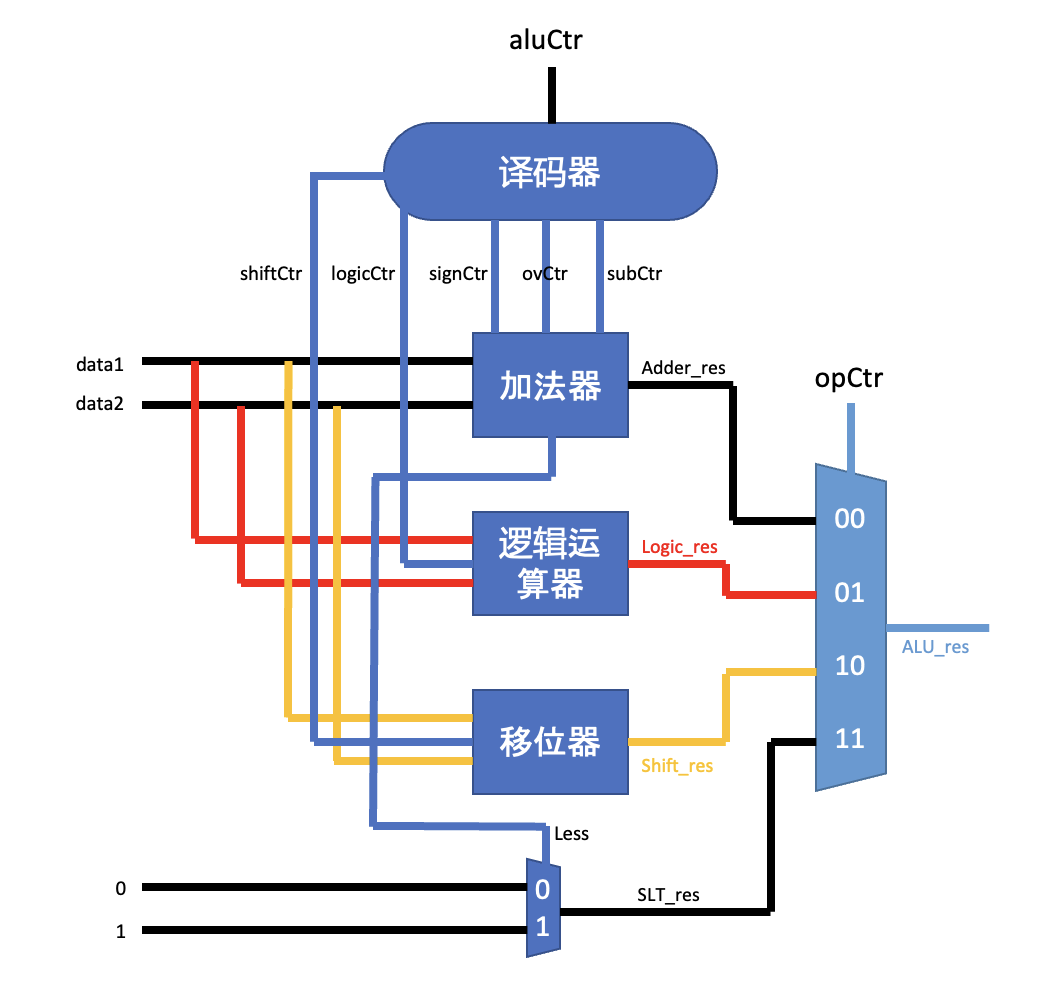
根据图示,我们就可以在 SpinalHDL 框架下设计出一个实现了 RV64I 指令集中运算部分功能的 ALU 了:
package alu
import spinal.core._
import spinal.lib._
class ALU extends Component {
val io = new Bundle {
val aluOp = in UInt (4 bits)
val data1 = in SInt (64 bits) //from rs1
val data2 = in SInt (64 bits) //from rs2 or immediate
val Zero = out Bool()
val aluResult = out SInt (64 bits)
}
noIoPrefix()
val counter = Reg(UInt(8 bits)) init (0)
counter := counter + 1
//get control signal for each module: Adder, Shifter, Logical calculator
val opCtr = UInt(2 bits)
switch(io.aluOp) {
is(U"4'b0000", U"4'b1000") {
opCtr := 0 //for Adder
}
is(U"4'b0001", U"4'b0010") {
opCtr := 1 //for SLT & SLTU
}
is(U"4'b0110", U"4'b0111", U"4'b1001") {
opCtr := 2 //for Shifter
}
is(U"4'b0011", U"4'b0100", U"4'b0101") {
opCtr := 3 //for logic calculator
}
default {
opCtr := 0
}
}
val signCtr = io.aluOp.mux(
U"4'b0010" -> False, //no need for adderSign
default -> True
)
val subCtr = io.aluOp.mux(
U"4'b0001" -> True, //True for subtraction
U"4'b0010" -> True,
U"4'b1000" -> True,
default -> False
)
val overflowCtr = io.aluOp.mux(
U"4'b0010" -> False, //no need for adderOverflow
default -> True
)
val shiftCtr = io.aluOp.mux(
U"4'b0110" -> U"2'b00", //SLL
U"4'b0111" -> U"2'b10", //SRL
U"4'b1001" -> U"2'b01", //SRA
default -> U"2'b00"
)
val logicCtr = io.aluOp.mux(
U"4'b0011" -> U"2'b00", //AND
U"4'b0100" -> U"2'b01", //OR
U"4'b0101" -> U"2'b10", //XOR
default -> U"2'b00"
)
//Adder & SLT
val adder = new Adder
adder.io.data1 := io.data1.asUInt
adder.io.data2 := subCtr ? ~io.data2.asUInt | io.data2.asUInt
adder.io.subCtr := subCtr
val adderOverflow = adder.io.overflow
val adderSign = adder.io.sign
val adderCarryOut = adder.io.carryOut
io.Zero := adder.io.zero
val adderResult = adder.io.adderResult.asSInt
//for SLT & SLTU
val sltLess = adderSign ^ adderOverflow
val sltuLess = ~adderCarryOut
val sltResult = (signCtr ? sltLess | sltuLess) ? S"64'b1" | S"64'b0"
//Shifter
val shifter = new Shifter
shifter.io.data := io.data1.asUInt
shifter.io.shamt := io.data2(4 downto 0).asUInt
shifter.io.shiftCtr := shiftCtr
val shiftResult = shifter.io.shiftResult.asSInt
//Logical calculator
val andResult = io.data1 & io.data2
val orResult = io.data1 | io.data2
val xorResult = io.data1 ^ io.data2
val logicResult = logicCtr.mux(
0 -> andResult,
1 -> orResult,
2 -> xorResult,
default -> S"64'b0"
)
io.aluResult := opCtr.mux(
0 -> adderResult,
1 -> sltResult,
2 -> shiftResult,
3 -> logicResult
)
}
object ALUVerilog {
def main(array: Array[String]): Unit = {
SpinalConfig(
mode = Verilog,
targetDirectory = "verilog/ALU"
).generate(new ALU)
}
}
在 ALU 模块设计完毕后,我们可以使用 SpinalHDL 框架中的仿真包,结合 iverilator 我们可以通过仿真测试模块功能以验证正确性:
package alu
import spinal.core._
import spinal.core.sim._
object ALUSim {
def main(args: Array[String]): Unit = {
SimConfig.withWave.compile(new ALU).doSim { dut =>
dut.clockDomain.forkStimulus(10)
SimTimeout(10000)
dut.clockDomain.waitSampling(10)
var data1 = 10
var data2 = 20
var aluOp = 0
//ADD SUB
dut.io.data1 #= data1
dut.io.data2 #= data2
dut.io.aluOp #= aluOp
dut.clockDomain.waitRisingEdge()
aluOp = 8
dut.io.aluOp #= aluOp
//SLT SLTU
dut.clockDomain.waitRisingEdge()
aluOp = 1
dut.io.aluOp #= aluOp
dut.clockDomain.waitRisingEdge()
data1 = -10
dut.io.data1 #= data1
dut.clockDomain.waitRisingEdge()
aluOp = 2
dut.io.aluOp #= aluOp
dut.clockDomain.waitRisingEdge()
data1 = 10
dut.io.data1 #= data1
dut.io.aluOp #= aluOp
//AND OR XOR
dut.clockDomain.waitRisingEdge()
data1 = 1
aluOp = 3
dut.io.data1 #= data1
dut.io.aluOp #= aluOp
dut.clockDomain.waitRisingEdge()
data1 = 65536
aluOp = 4
dut.io.data1 #= data1
dut.io.aluOp #= aluOp
dut.clockDomain.waitRisingEdge()
data1 = 10
data2 = 15
aluOp = 5
dut.io.data1 #= data1
dut.io.data2 #= data2
dut.io.aluOp #= aluOp
//SLL SRL SRA
dut.clockDomain.waitRisingEdge()
data1 = 128
data2 = 2
aluOp = 6
dut.io.data1 #= data1
dut.io.data2 #= data2
dut.io.aluOp #= aluOp
dut.clockDomain.waitRisingEdge()
data1 = -2
aluOp = 7
dut.io.data1 #= data1
dut.io.aluOp #= aluOp
dut.clockDomain.waitRisingEdge()
aluOp = 9
dut.io.aluOp #= aluOp
dut.clockDomain.waitRisingEdge()
simSuccess()
}
}
}
仿真结果如下:


可以看到,ALU 通过了所有功能的测试。
状态元件是时序逻辑电路的基本组成单元,在 CPU 设计中主要的模块是:
- 通用寄存器组
- 存储器
由于存储器可以直接调用赛灵思的 IP 核结合 FPGA 核心板直接使用,故本节将主要介绍通用寄存器组的设计。
通用寄存器组
在 SpinalHDL 框架里,寄存器有专门的关键词 Reg 可以直接定义得到,其表现为在时钟有效边沿到来时根据 := 赋值语句对寄存器内数据进行更新。有了这一便捷操作寄存器的特性,我们就只需要考虑通用寄存器组的整体设计方案了。
在 RV64I 指令集架构中,32 个通用寄存器都是位宽 64 位;根据 RV64I 中对指令形式的规定,我们可以看到:
- 每条位宽为 32 位的指令至多读取 2 个寄存器
- 每条位宽为 32 位的指令至多写入 1 个寄存器
- 不是所有的指令都会进行写入寄存器的操作
所以,在设计通用寄存器组模块时,这一模块在读取操作上需要 2 个读取数据端;在写入操作上需要 1 个写入数据端;而为了保证能满足指令对写入操作可控,我们还需要一个使能信号对通用寄存器组模块的写入操作进行限制。最终我们可以用画图的方法展示一个通用寄存器组的基本结构:
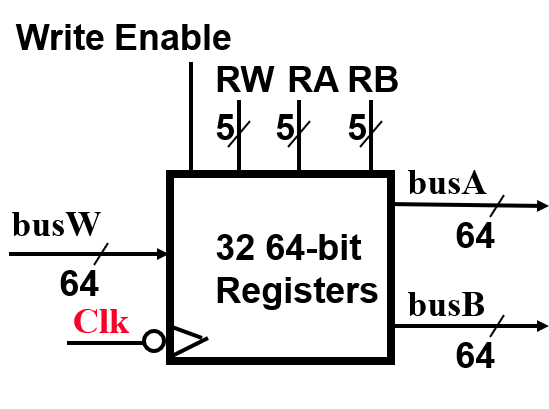
- 2 个读取数据端(组合逻辑电路):从 RA 和 RB 两个输入的寄存器地址(即寄存器编号)寻找到对应通用寄存器,读取数据后分别送至 busA 和 busB 两个输出端。地址 RA 和 RB 有效后,经过一个取数时间(Access Time),busA 和 busB 数据线有效
- 1 个写入数据端(时序逻辑电路):当写入使能(Write Enable)为 1 时,有效时钟边沿到来时,busW 数据线上的数值开始写入 RW 地址指定的寄存器中
通用寄存器组的内部结构如下图所示:
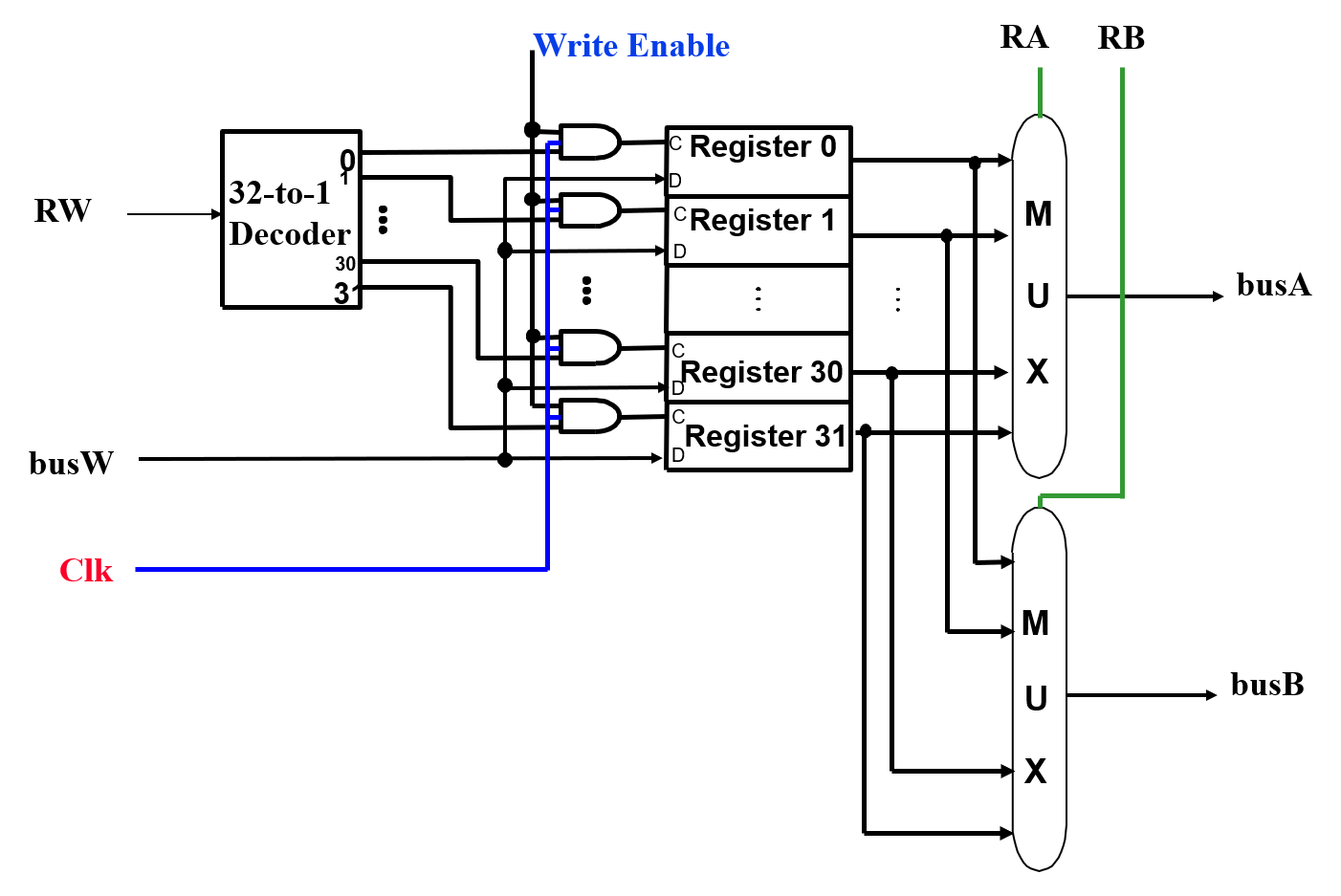
所以,根据画出的设计图,我们就可以在 SpinalHDL 框架下设计出自己的通用寄存器组了:
package reg
import spinal.core._
import spinal.lib._
class Register_file extends Component {
val io = new Bundle {
val RegWrite = in Bool() // Enable Signal
val readReg1 = in UInt (5 bits)
val readReg2 = in UInt (5 bits)
val writeReg = in UInt (5 bits)
val writeData = in UInt (64 bits)
val readData1 = out UInt (64 bits)
val readData2 = out UInt (64 bits)
}
noIoPrefix()
//Define 32 general registers
val Regs = Vec(Reg(UInt(64 bits)) init(0), 32)
//Read Data
io.readData1 := Regs(io.readReg1)
io.readData2 := Regs(io.readReg2)
//Write Data
when(io.RegWrite) {
//In fact, here is a trigger. So if you want to pause at anytime, just add "when(~pause signal){do sth..}otherwise{pause..}
Regs(io.writeReg) := io.writeData
}
}
object Register_fileVerilog {
def main(args: Array[String]): Unit = {
SpinalConfig(
mode = Verilog,
targetDirectory = "verilog/Register_file"
).generate(new Register_file)
}
}
同样的,我们可以利用 SpinalHDL 框架下的仿真模块,对通用寄存器组模块进行仿真验证:
package reg
import spinal.core.sim._
// Register_file's testbench
object Register_fileSim {
def main(args: Array[String]): Unit = {
SimConfig.withWave.compile(new Register_file).doSim { dut =>
//get clock
dut.clockDomain.forkStimulus(10)
SimTimeout(10000)
dut.clockDomain.waitSampling(10)
for (i <- 1 to 20) {
//test write
dut.io.writeReg #= i + 1
dut.io.writeData #= i + 1
if (i < 10) {
dut.io.RegWrite #= true
} else {
dut.io.RegWrite #= false
}
//test read
dut.io.readReg1 #= i
dut.io.readReg2 #= i - 1
dut.clockDomain.waitRisingEdge()
if (i == 7) {
dut.clockDomain.assertReset()
} else {
dut.clockDomain.deassertReset()
}
}
simSuccess()
}
}
}
仿真结果如下:

可以看到,我们设计的通用寄存器组很好的完成了所有的功能,测试通过。
总结
本文首先介绍了 CPU 设计的理论相关知识,将数据通路的基本功能与结构进行了讲解,后半部分细致的介绍了数据通路中主要模块的设计思路与实现方法。
系列文章预告:单周期 CPU 数据通路的搭建与简单 RISC-V 汇编程序的运行。
参考资料
计算机组成与设计:硬件/软件接口(第五版)戴维 A. 帕特森 约翰 L. 亨尼斯 著
CPU 设计实战 汪文祥 邢金璋 著
本文部分图片来自参考资料(Wiki 和 RISC-V 手册等),感谢原作者的辛苦工作!
猜你喜欢:
- 我要投稿:发表原创技术文章,收获福利、挚友与行业影响力
- 知识星球:独家 Linux 实战经验与技巧,订阅「Linux知识星球」
- 视频频道:泰晓学院,B 站,发布各类 Linux 视频课
- 开源小店:欢迎光临泰晓科技自营店,购物支持泰晓原创
- 技术交流:Linux 用户技术交流微信群,联系微信号:tinylab
| 支付宝打赏 ¥9.68元 | 微信打赏 ¥9.68元 | |
 |  请作者喝杯咖啡吧 |  |
Read Album:
- Stratovirt 的 RISC-V 虚拟化支持(六):PLIC 和 串口支持
- Stratovirt 的 RISC-V 虚拟化支持(五):BootLoader 和设备树
- Stratovirt 的 RISC-V 虚拟化支持(四):内存模型和 CPU 模型
- Stratovirt 的 RISC-V 虚拟化支持(三):KVM 模型
- Stratovirt 的 RISC-V 虚拟化支持(二):库的 RISC-V 适配