红黑树 IN Linux （三）

Chen Jie 创作于 2016/10/07

By Chen Jie of TinyLab.org 2016-10-07 21:11:17

前言：

本系列的第一篇，回顾了红黑树的 5 个约束条件，以及 Linux 实现的红黑树额外拥有的俩特性：lockless lookup 和 augment。第二篇，展示了删除红黑树的一个节点，如何“再平衡”。本篇将展示，向红黑树中添加一个节点，如何“再平衡”。

下图展示了向红黑树中添加一个节点的两种情形：

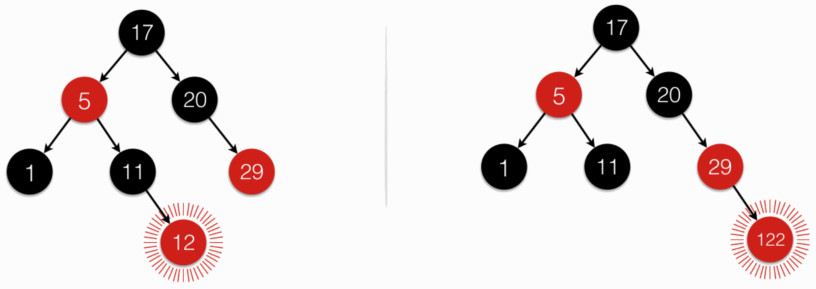
图中，用 辐线包裹 来标识新添加的节点：

左边：新加入节点“12”，恰好仍满足红黑树 5 个约束条件，无需“再平衡”。
右边：新加入节点“122”，破坏了红黑树约束条件 4，需“再平衡”。

前篇为方面描述，将没有子节点（或说子节点都是 NULL）的节点称为“叶子节点”；只有一个子节点的（或说某个子节点是 NULL）的节点称为“半叶节点”。

此处可见，新添加的节点，总是在 “（半）叶节点”上。这是因为，红黑树的任一节点，在排序中，其前一节点为 左子树中最右的（若左子树存在）；其后续节点为 右子树中最左的（若右子树存在）。而所谓“最右”或“最左”，实际上就是“（半）叶节点“（不然还有左/右子，就不是最左或者最右啦）。

由上图，向红黑树添加一个节点，可能导致约束条件 4 违例，需“再平衡”，以下讨论此过程。

红黑树：添加一个节点

我们从一个函数调用栈入手：

// http://lxr.free-electrons.com/source/lib/rbtree.c?v=4.8#L418
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
	__rb_insert(node, root, dummy_rotate);
}

参数一为新添加的节点，该节点的加入可能导致约束条件 4 违例，需本函数来“再平衡”。

实际干活的函数 __rb_insert，其骨架为：

// http://lxr.free-electrons.com/source/lib/rbtree.c?v=4.8#L97
__rb_insert(struct rb_node *node, struct rb_root *root,
	...)
{
	struct rb_node *parent = rb_red_parent(node), *gparent, *tmp;
 
	while (true) {
		/*
		 * Loop invariant: node is red
		 *
		 * If there is a black parent, we are done.
		 * Otherwise, take some corrective action as we don't
		 * want a red root or two consecutive red nodes.
		 */
		if (!parent) {
			rb_set_parent_color(node, NULL, RB_BLACK);
			break;
		} else if (rb_is_black(parent))
			break;
 
		gparent = rb_red_parent(parent);
 
		tmp = gparent->rb_right;
		if (parent != tmp) {	/* parent == gparent->rb_left */
			...
		} else {		/* parent == gparent->rb_right */
			...
		}
	}
}

一些隐含的前提为：

新加入的节点 —— node 天然地设为红色
若 node 的 parent 为红色，则违反约束条件 4，正是本函数用武之地。
若 node 的 parent 为红色，则根据约束条件 2，必有 grandparent。

根据 parent 为 grandparent 左子，还是右子，分成两大块处理。两块的处理流程是对称的。

下面以 parent 在右为例，阐述代码中的 Case1 - Case3。

Case1

当 parent 的兄弟节点为红色时，落在 Case1。注意，据约束条件 4，grandparent 为黑色。

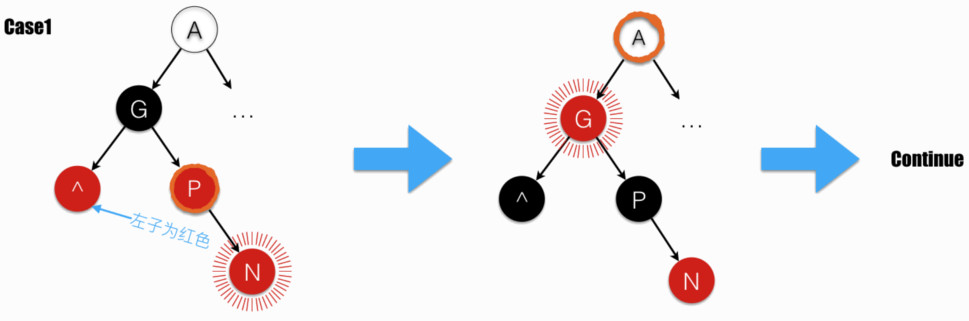
此时，交换 grandparent 和其两子的颜色，再进入下一轮循环。

注意，图中 parent 用 橙色墨迹 圈出。

Case2 和 Case3

Case2：parent （橙色墨迹 圈出）的兄弟节点为黑（或不存在，即 NULL - 严格意义上的叶节点。按照红黑树约束条件 3 定义，叶节点都是黑色）；且 node （辐线包裹）为 parent 的左子。
Case3：parent （橙色墨迹 圈出）的兄弟节点为黑（或不存在）；且 node （辐线包裹）为 parent 的右子。

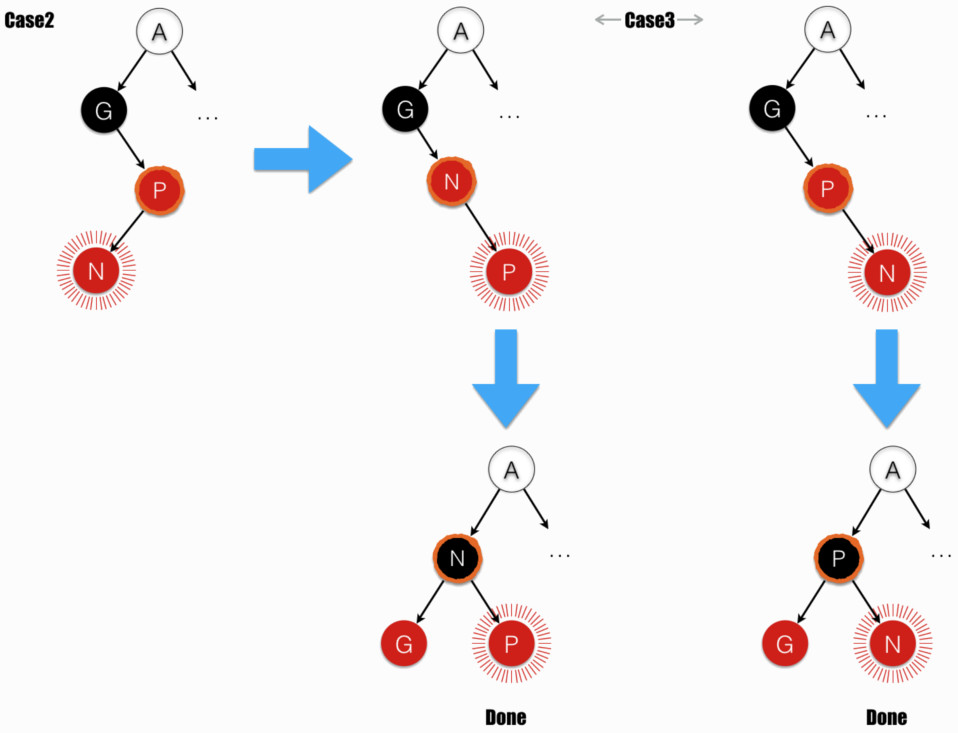
Case2 在 parent 上进行右旋，变化到了 Case3。注：图中伴随右旋，parent（橙色墨迹 圈出）由 P 变为 N；node（辐线包裹）由 N 变为 P。

Case3 在 grandparent 上进行左旋。注：旋转操作同时交换位置和颜色。

最终达“平衡”。

后记：再看 lockless

在本系列第一篇中，介绍lockless lookup 中，提到单靠 父向子指针 的原子访问，准确性仍有失。为达到一致的准确性，出现了 latch 版本的红黑树：

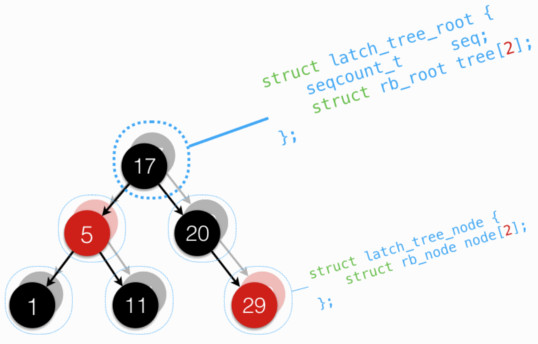
latch 版本红黑树，借助 seqlock，来达到多个读者和一个写者的并发访问：

维护两个红黑树，更新时依次更新
- 先增 seqcount，此处改变了奇偶，让随后读者先去访问另一（不在更新的）树。

// http://lxr.free-electrons.com/source/include/linux/rbtree_latch.h?v=4.8#L142
latch_tree_insert(struct latch_tree_node *node,
                  struct latch_tree_root *root,
                  const struct latch_tree_ops *ops)
{
        raw_write_seqcount_latch(&root->seq);
        __lt_insert(node, root, 0, ops->less);
        raw_write_seqcount_latch(&root->seq);
        __lt_insert(node, root, 1, ops->less);
}

读者访问其中一树，通过比对 seqcount，确认返回结果是否准确。
- 具体该访问哪棵树？选择索引为 seqcount & 1 的树，该树大概率下不在更新中。

// http://lxr.free-electrons.com/source/include/linux/rbtree_latch.h?v=4.8#L197
static __always_inline struct latch_tree_node *
latch_tree_find(void *key, struct latch_tree_root *root,
                const struct latch_tree_ops *ops)
{
        struct latch_tree_node *node;
        unsigned int seq;

        do {
                seq = raw_read_seqcount_latch(&root->seq);
                node = __lt_find(key, root, seq & 1, ops->comp);
        } while (read_seqcount_retry(&root->seq, seq));

        return node;
}

留意：

latch 版本的红黑树，限制了红黑树的更新和查找 —— 需指定一组 “visitor 函数”。这就好比某结构体的遍历方式，原是宏版本的 FOREACH；现在改成了函数版本的 foreach，需要传入 “visitor 函数”。
各种访问临界区的方式：

第 2 点中细节处，颇有些趣问题，比如

raw_write_seqcount_latch 为啥不写成原子操作（WRITE_ONCE）？特别是再对比读端 raw_read_seqcount_latch 和 read_seqcount_retry，一个是 READ_ONCE，一个不是。
rcu_assign_pointer 为啥写得如此复杂？
各种访存 barrier(s)（smp_wmb/smp_read_barrier_depends/smp_rmb/mb）区别是啥？
…

后记：加入! Linux hacking

浏览了这许多代码，是否也跃跃欲试了呢？想要试验下，搞明白代码行为？？或是发现了代码中的瑕疵和缺陷，想要向官方提补丁？

首先，需要试验 / 验证你的补丁，这时可在虚拟机中运行补丁后的内核。。。那么问题来了，怎么方便地搭建试验环境呢？不妨试试本站「基于 Docker/Qemu 快速构建 Linux 内核实验环境」一文。

接下来，想要向社区提交你的补丁？Linux 内核社区是一个健全的开源社区，有许多制度来保障良性发展。若要合作愉快，就需了解其中规范。本站「Linux upstream: 给 Linus 发个 patch 吧」一文中，几位社区的开发者现身说法，结合规范文档，丰富叙述此事。

最后，如果你用着程序员最爱的 gmail 邮箱，如何让 git send-email 透过 gmail 发补丁呢？首先启用 google 账户的两步验证，接着为本地 git 连上 gmail，设置一个专用密码；然后配置 git

# vi ~/.gitconfig
[sendemail]
	from = Your Name <yourname@gmail.com>
	smtpencryption = tls
	smtpserver = smtp.gmail.com
	smtpuser = yourname@gmail.com
	smtpserverport = 587

配置好了，现在，将补丁发出：

$ git send-email --cc=somebody@xxx --cc=somebody@yyy --to=somemailinglist@zzz the_patch.patch

# 首次发送，会提示输入密码，输入前述专用密码即可
#   git 会通过 git credential，自动将密码保存在 *密钥环管理器* 中。
# 如出错，可在 send-email 之后，紧跟一个 --smtp-debug=1 来看下具体细节

后记：树、面试与找工作

较为遗憾的是，工作这些年来，几乎没有接触和显式地用到树。这种情况，估计也不算个例。因此，从实用角度而言，也许也只在面试环节，会遇上树这类话题吧。

聊到面试，就来了永恒的话题，找工作，或者更高级地说法 —— “职业规划”。这个过程，是这样的：

首先，看到各式各样的职位描述（JD），大体特点是非常细分、专业化的。但对于刚刚走出校园的学生，或是像笔者这样的，信仰技术的通透和通用，更注重这方面的积累和成长。事实上，优秀公司的职位，是专业细分的；但卓越公司的职位，却是返璞归真，反过来强调应聘者的技术通透性，这点可参见 google 的 JD。

从笔者的经历而言，将通用能力的成长，又分为俩方面

“蓝色”能力的成长：这是对职场范式的掌握程度。
比如，看到企业中一个任务是怎么运作的：包括它的投入产出评估、时间计划（没错，许多情况是看着时间排任务，而不是任务多少排时间）、任务分解、阶段目标设定、核对完成状况与妥协、响应新变化以及最后的绩效考核。
对于个人，比如团队协作，沟通如何达意；面对异议，如何坚持与妥协；如何面对质疑；如何面对情绪；如何信任与放权，却又产出符合预期；如何保留余地。
又比如连续高强度地工作，能力极限在哪；如何聚焦；如何恢复精力。
再比如对所处理业务的估计能力，条件发射式地对应到时间代价，精力代价（嗯，不是人力，是精力。有些粗糙管理，看员工是否深度加班，对大多数人而言，连续大强度加班，精力下降，好比一场球赛中的垃圾时间。。。），以及是否可行（说“不可行“可比其他答案要难得多）。
“橙色”能力的成长：这是技术能力的成长。
比如更广泛地了解技术，所谓全栈工作能力。
更深入地了解技术，深知计算机体系结构，从而举一反三、融会贯通。
有了广度和深度，便能在不同的域架起“桥”，便有了创造，并体验了创造的乐趣。
创造是乐，但也许最终未成型，变为失落；乐乐忧忧喜喜悲悲，终于看淡，得释心，便有了宏观架构上的敏锐感觉。

初入职场，选择一个大公司，能有效锻炼“蓝色”能力，知道职场范式，知道公司如何依据范式招聘，从而也知道如何按照范式强化己的竞争力，最终能更好流动于职场的未来工作机会中 —— 但，另一角度而言，这也是个格式化的过程（或说，职业认知的定形）

而选择一个创业型的小公司，则“蓝色”能力成长也许并不全面；但“橙色”能力成长则较显著 —— 创业公司并非高度分工，因此有对技术全景了解的机会。机会给予了特别视角（或氛围），从而可能突破认知局限，更上一层楼。

另一方面，抛开上述这些宏观论调，面试中会有哪些着眼点呢？这里粗略地捡三点，更多观点欢迎在评论区里点燃:)

关注自由度：
自由度一方面是指工作中能表达和实践己见的程度，俗语“既要马儿跑又要马儿不吃草”是一个自由度极低的例子。
自由度的另一方面，是关于状态锁定的 —— 当缺乏第一方面自由度的工作占据了全部精力，以至于无暇作出改变，从而现状维持的情形。
了解面试官（特别是经历相似的）加入企业后的发展历程，侧面了解状态锁定的程度。
关注团队的直属领导：
他/她是否具备技术上洞察力；是否认同其技术感觉和判断；是否认同其行事方式等。
了解面试职位所在团队信息，了解面试官在团队中的角色，倾听他们各自对团队的观点，从各个侧面来了解此处关注。
企业大环境也许并不高歌猛进，但好的团队领导却能让人受益非浅；反之，即便在一个奋进的企业，团队也处地融洽，一个技术和行事风格与己相左的团队领导，会造成工作上相当的困难。
关注企业史：
企业是怎样活下来，通常地，就会怎样活下去。
如何获得第一桶金，如何孵化出第一个养活的业务，这些经历会成为基因一样的东西留在企业 —— 这也许不能直接感受到，却在一段时间后，成为看不见的墙一样的存在。
了解企业史，更好地预见在企业中的发展，从长计议。

附加题：google 面试十问

领英上瞧见的转帖：「google 面试十问」大体表达过于细末，似孔乙己问“茴字的几种写法“。此处转载，就着上节进一步铺陈、并制造一些沉浸感 :)

1. What is the opposite function of malloc() in C?

2. What Unix function lets a socket receive connections?

3. How many bytes are necessary to store a MAC address?

4. Sort the time taken by: CPU register read, disk seek, context switch, system memory read.

5. What is a Linux inode?

6. What Linux function takes a path and returns an inode?

7. What is the name of the KILL signal?

8. Why Quicksort is the best sorting method?

9. There’s an array of 10,000 16-bit values, how do you count the bits most efficiently?

10. What is the type of the packets exchanged to establish a TCP connection?

附上个人答案，供参考，误请不吝吐槽：

1. What is the opposite function of malloc() in C?

free()，简单吧。

2. What Unix function lets a socket receive connections?

accept() 啦。面向连接的标准编程步骤：server bind() 并 listen()，然后阻塞在 accept() 上，当 client connect() 来时，server 处 accpet() 返回一个建立好的连接。

3. How many bytes are necessary to store a MAC address?

MAC 地址是 48 位，6 字节。顺便问一句，记得 IPv4 地址多少位吗？IPv6 呢？答案是 32 位（4 字节）和 128 位（16 字节）。

4. Sort the time taken by: CPU register read, disk seek, context switch, system memory read.

读寄存器最快；读内存次之；然后是上下文切换（上下文切换也要访存，故不可能比读内存快）；最慢的是磁头寻址，该会发生上下文切换来让出 CPU。

5. What is a Linux inode?

文件对象（普通文件，设备节点，socket 和 pipe 节点）的节点，存有对象的元数据。

6. What Linux function takes a path and returns an inode?

这该是说内核的函数吧？kern_path() 然后取path.dentry->d_inode？

7. What is the name of the KILL signal?

KILL 是用来强制杀掉进程的信号（只要进程不在不可中断睡眠，均可被杀），它，它。。。有 name 吗？是说 9 吧？？

8. Why Quicksort is the best sorting method?

Quicksort 性能最优为 O(nlog n)，最差为 O(n^2)；空间复杂度（递归调用）最坏为 O(log n)。其有力的竞争对手为 Heapsort，性能表现更稳定 —— 最差情形也为 O(nlog n)，空间复杂度为 O(1)。

但实践中，通常 Quicksort 性能更好，因算法能优化实现，例如访存的局部性好，详见这篇：Why is quicksort better than other sorting algorithms in practice?。

下面贴一些细节，回忆下 Quicksort 算法：

# 伪代码来自 https://en.wikipedia.org/wiki/Quicksort
algorithm quicksort(A, lo, hi) is
if lo < hi then
    p := partition(A, lo, hi)
    quicksort(A, lo, p – 1)
    quicksort(A, p + 1, hi)

在一组数中，partition() 函数挑其中一数（pivot）来分组：小于等于 pivot 的在左（数组索引的区间为“[lo-p)”）；大于 pivot 的在右（数组索引的区间为“(p-hi]”）。两组再分别递归调 Quicksort。下图为经典 partition 函数的示意：

上图中，i 追着 j。在改进的 partition 函数中，i 和 j 相向而遇：

留意此 partition 方法中，pivot 并不居中：小于等于 pivot 的在左（数组索引的区间为“[lo-p]”）；大于 pivot 的在右（数组索引的区间为“(p-hi]”）。

如果运气够好，开始、及之后每次递归选的 pivot 都将数组 近乎二等分，则长度为 n 数组，排序经历 log n 层。每层中的各区段，再一分为二（partition）需遍历区段内各元素，全部区段粗算需遍历 n 个元素。粗计为 nlog n，故而性能最优为 O(nlog n)。相反，运气够背，开始选的 pivot 将数组分为 1 和 n - 1 两部分，之后每次递归恰好也是，则经历 n - 1 层。每层全部区段粗算需遍历 n 个元素，粗计为 n(n - 1)，故而性能最差为 O(n^2)。

由此可见 pivot 的选择很重要。实践中，采用“分段取中位数再取中位数”，或是随机选择（pivot 选择应用到上图俩 partition 方法：将选中的数与数组尾数对调即可）。

最后，Quicksort 空间复杂度，来自递归的空间开销。这里引一概念 —— “尾递归”，是指函数结尾处有递归调用 —— 函数执行尾递归时，没必要再垒起一 函数调用帧，而是直接复用当前帧。现规定尾递归的 Quicksort 总是处理 分出两段中最长的一段 —— 当每次递归分出两段均等时，递归深度为 log n 次，故空间开销为O(log n)，这是空间复杂度的最坏，却也是性能上的最优；另一方面，当每次递归分出两段，分别是 1 和 rest（余下元素）时，由于按规定较长的 rest 尾递归处理掉了，故空间复杂度为 O(1)，这是空间复杂度的最好，却也是性能上的最差。

9. There’s an array of 10,000 16-bit values, how do you count the bits most efficiently?

本问题问，数组中置 1 的位有多少？这是考较对计算机指令、二进制运算的理解。首先最直接的：x86 上，带有 SSE4 的处理器，同时支持 POPCNT 指令：数整数中置上 1 的位数。

但如用纯 C 实现，优化的实现是怎样的？

int popcount_1(uint64_t x) {
①   x = (x & m1 ) + ((x >>  1) & m1 ); // m1  的二进制形式为 01 01 01...
②   x = (x & m2 ) + ((x >>  2) & m2 ); // m2  的二进制形式为 0011 0011 0011 ...
③   x = (x & m4 ) + ((x >>  4) & m4 ); // m4  的二进制形式为 0000 1111 0000 1111 ...
④   x = (x & m8 ) + ((x >>  8) & m8 ); // m8  的二进制形式为 00000000 11111111 ...
     
    // m16 的二进制形式为 0000000000000000 1111111111111111 ...
⑤   x = (x & m16) + ((x >> 16) & m16);
     
    // m32 的二进制形式为 00000000000000000000000000000000 11111111111111111111111111111111
⑥   x = (x & m32) + ((x >> 32) & m32);
    return x;
}
 
// 图示如下：

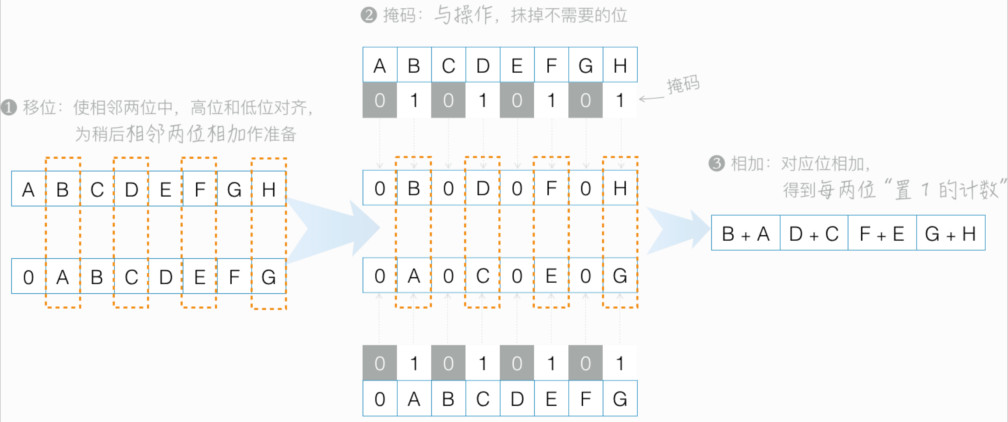
// 进一步优化上面的 C 实现
首先 ①  可以改写成 x -= (x >> 1) & m1  /* 第一反应：卧槽，什么鬼？
* 二进制减法是 被减数 + 减数的相反数
* 一个数的相反数是按位取反 + 1，或者 "{高位按位取反}{100...0 保持不变}"
* “与上 m1，再取相反数”后，其模式为 "{11, 10} 11 {0}"（或 "全零"，最简单故不提）
*
* 上述模式，中间的 "11" 对应原数中 "10" 或 "11"：
*   11 + 10 = 101；11 + 11 = 110，特点是均有进位；此外，“1”计数正确。　
*
* 上述模式，“11” 左边，是 "11" 和 "10" 的重复：
* "11" 对应原数中的 "00" 或 "01": 11 + 00 + 1（进位）= 100; 11 + 01 + 1（进位）= 101
* "10" 对应原数中的 "10" 或 "11"：10 + 10 + 1（进位）= 101; 10 + 11 + 1（进位）= 110
* 特点是总有进位；此外，“1”计数正确。
*/
 
其次 ③  可以写成 x = (x + (x >> 4)) & m4 /* 4bits 中的 “1” 计数，最多为 100
* 这样，在按 8bits 合计的过程中，即便没有掩去高位，也无溢出（最大 100 + 100 = 1000，还是 4bits）
*/
 
最后 ⑤  和 ⑥  可以写成 x = (x * h01_mask) >> 56 /* h01_mask = 0x0101010101010101
* h01_mask 二进制为 0000 0001 0000 0001 ...
* 二进制乘法，是一个“移位加”的过程，比如 y = 0010, y * 0101：
*   0000  # (0010 * 0) << 3
*   1000  # (0010 * 1) << 2
*   0000  # (0010 * 0) << 1
* + 0010  # (0010 * 1) << 0
* = 1010
*
* 故 x * h01_mask = x + x << 8 + x << 16 + x << 24 + x << 32 + x << 40 + x << 48 + x << 56
* 即逐步把每个 8bits 都移到“最高 8bits”，然后累加在“最高 8bits”。
* 比如：x + x << 8 是把“次高的 8bits”移至最高，累加在“最高 8bits”
*       ... + x << 56 是把“最低的 8bits”移至最高，累加在“最高 8bits”
* 另注意 8bits 累加不会溢出 8bits
*/
 
以上优化整理后，就成了：
int popcount_3(uint64_t x) {
⑦   x -= (x >> 1) & m1;
    x = (x & m2) + ((x >> 2) & m2);
    x = (x + (x >> 4)) & m4;
    x = (x * h01_mask) >> 56;
    return x;
}
 
 
// 若“1” 较为稀疏，则存在另一种优化实现：
int popcount_4(uint64_t x) {
    int count;
    for (count=0; x; count++)
        x &= x-1;
    return count;
}

/* 当最低位为 1，此时无需借位
    x &= x-1，仅计入一个“1”，同时 x 最低位清 0。
 * 当最低位为 0，此时需向高位借位，比如 x = ???? 1000; x-1 = ???? 0111;
    x &= x-1 之后，x 为 ???? 0000，由此可见该算法的效率
 */

上述优化后的实现，popcount_3总共 12 条 算术指令，其中有 1 条乘法指令；popcount_4每个“1”用 3 条 算术指令 和 1 条 条件分支指令。作为对比，popcount_1总共有 24 条算术指令。

最后，来个大综合。假设当前 CPU 不支持“POPCNT”指令，但有 SSE2 指令。如何利用 SSE2 来最优实现？下面答案来自 Quora：

循环策略：
1. 内层循环 10 次，每次处理 3 * 128bits 数据，借助变量 acc 累加到 ct
2. 由上，内层循环完，处理掉 10 * 3 * 128bits 数据，即 30 * 8 * 16bits；故外层循环次数为：array_len / (30 * 8)
3. 余下不足喂饱“内层循环”的，交由 popcount_3() 来处理。
用到的 SSE2 指令简介：
1. __m128i _mm_add_epi64(__m128i a, __m128i b) 将 a 的两个 64bits 与 b 对应 64bits 相加
2. __m128i _mm_srli_epi64 (__m128i a, int count) 将 a 的两个 64bits 分别右移 count 位（头补 0）
3. __m128i _mm_and_si128 (__m128i a, __m128i b) 128bits “与操作”
4. __m128i _mm_sub_epi64 (__m128i a, __m128i b) 将 a 的两个 64bits 减去 b 对应 64bits
5. __m128i _mm_setzero_si128 () 128bits 置 0
下面来关注内层循环：

...
__uni128 acc.vi = _mm_setzero_si128();
for (sub_loop_iters = 0; sub_loop_iters < 10; sub_loop_iters++) {
    // count1：从数组取本轮循环的第一个 128bits
    // count2: 从数组取本轮循环的第二个 128bits
    // count3: 从数组取本轮循环的第三个 128bits
     
    // half1: count3 的偶数位（第零位算起）
    // half2: count3 的奇数位（并移位到偶数位）
    half1 =  _mm_and_si128(count3, m1);
    half2 = _mm_and_si128(_mm_srli_epi64(count3, 1), m1);
     
    // 同时对俩 64bits 做 `⑦  of popcount_3()`
    count1 = _mm_sub_epi64(count1,
                           _mm_and_si128(_mm_srli_epi64(count1, 1), m1));
    // 含义同上
    count2 = _mm_sub_epi64(count2,
                           _mm_and_si128(_mm_srli_epi64(count2, 1), m1));
     
    // count3 的偶数位 “1”，计入到 count1 对应 2bits
    count1 = _mm_add_epi64(count1, half1);
    // 类上。注意：累加无溢出，最大可能值恰好为 2bits 最大数值“11”
    count2 = _mm_add_epi64(count2, half2);
     
    // 老套路，见 ② 
    count1 = _mm_add_epi64(_mm_and_si128(count1, m2),
                           _mm_and_si128(_mm_srli_epi64(count1, 2), m2));
    count2 = _mm_add_epi64(_mm_and_si128(count2, m2),
                           _mm_and_si128(_mm_srli_epi64(count2, 2), m2));
    // 累加到 count1 上，注意累加前，每 4bits 最大可能值为“11 + 11 = 110”
    // 累加后，每 4bits 最大值为“110 + 110 = 1100”
    count1 = _mm_add_epi64(count1, count2);
     
    // 老套路，见 ③ ，但注意每 8bits 最大可能值现在是“1100 + 1100 = 11000”啦 
    count1 = _mm_add_epi64(_mm_and_si128(count1, m4),
                           _mm_and_si128(_mm_srli_epi64(count1, 4), m4));
     
    // typedef union {
    //     __m128i vi;
    //     uint64_t u64[2];
    // } __uni128;
    acc.vi = _mm_add_epi64(acc.vi, count1);
    // 至此，才统计完每 8bits 的“1”数，没有最后汇总
}

// 10 轮循环完，每 8bits 最大可能值，现在是十进制的 240（8bits 最大表达数 255）
// 此处终于憋不住了。。。进行后续累加，不然溢出啦

// 老套路，见 ④ 
acc.vi = _mm_add_epi64(_mm_and_si128(acc.vi, m8),
                       _mm_and_si128(_mm_srli_epi64(acc.vi, 8), m8));
 
// cee1: 此处开始，我有个微小的优化，见文末
// 套路 ⑤  演化过来的，由于不担心溢出（一个 16bits 足够表达 “每 32bits 最大可能值：960”）
// 所以先加，再掩码
acc.vi = _mm_and_si128(_mm_add_epi64(acc.vi,
                                     _mm_srli_epi64(acc.vi, 16)),
                       m16);
 
// 套路 ⑥  演化过来
// 注意最后没掩码，这是因为 ct 是 32bits，强制转换中，高位自然抛弃
acc.vi = _mm_add_epi64(acc.vi, _mm_srli_epi64(acc.vi, 32));
 
// 咱是 128bits，故多一步“将俩 64bits 再合计”
// 强制转换，抛掉了高 32bits
ct += (uint32_t)(acc.u64[0] + acc.u64[1]);

上述 SSE2 实现，末尾可以再做半步优化：

// 一个 16bits 足够表达 “每 128bits 最大可能值：128 * 30 = 3840”
acc.vi = _mm_add_epi64(acc.vi, _mm_srli_epi64(acc.vi, 16));
acc.vi = _mm_add_epi64(acc.vi, _mm_srli_epi64(acc.vi, 32));

ct += ((uint32_t)(acc.u64[0] + acc.u64[1])) & 0xffff;

// Net effect: 用一条算术指令代替一条 SSE2 指令。

最后，上述优化并未考虑输入数组的 地址对齐 情况，在实践中还需考虑“升级到”最佳对齐（本例中为 128bit），如「汇编实战：龙芯处理器之 memcpy 优化」一文所展示的那样。

10. What is the type of the packets exchanged to establish a TCP connection?

著名的三次握手：C: SYN；S: SYN-ACK；C: ACK。顺便问一句，怎么终结 TCP 连接？四次握手，任意一方发 FIN，应答方 ACK，再发 FIN，一开始“挑事那方”最后 ACK。

[置顶] 泰晓 RISC-V 实验箱，配套 30+ 讲嵌入式 Linux 系统开发公开课