“茴”字有几种写法：系统负载是怎样计算的？（一）

By Chen Jie of TinyLab.org 2017-06-25 00:25:17

前言

简单说，机器学习中的 “机器” 就是统计模型，“学习” 就是用数据来拟合模型。

「初探计算机视觉的三个源头、兼谈人工智能｜正本清源」，朱松纯（Song-Chun Zhu），加州大学洛杉矶分校 UCLA 统计学和计算机科学教授

大数据时代，统计很重要。通过统计事件、定期采样，定量评估现在，对比过去，预测将来。

系统负载，以及 CPU 利用率，也是统计得到的指标。指标对实际的拟合情况分好与更好，比如在近月，大名鼎鼎的 Linux 系统调优专家 Brendan Gregg 对现有 CPU 利用率统计提出了质疑，言其误导用户。

然而，诸如系统负载目下是如何统计的？—— “不就是个 C 实现的公式吗？” —— 这似乎是一个细究 “茴” 字有多少种写法的问题。

然而，吃掉一大块油腻腻新知识，不妨先从小处入手，追本溯源，知微见著。

本系列第一部分从 /proc/loadavg，来看该场景下的负载定义与计算。公式不是重点，内核常见的定点拟浮点会剐蹭下，而 tick 则成为浮光掠影般的沿途风景。

/proc/loadavg

# cat /proc/loadavg
# 0.20 0.18 0.12 1/80 11206

• 前三个数代表过去 1 / 5 / 15 分钟内，所有处于 就绪（等待和使用 CPU 资源）和 不可中断睡眠（等待和使用 IO 资源）的平均任务数，即平均负载。
• “1/80” 表示当前 1 个 任务就绪，总共 80 个任务。
• “11206” 代表最近一次分配出的 process ID 是 11206。

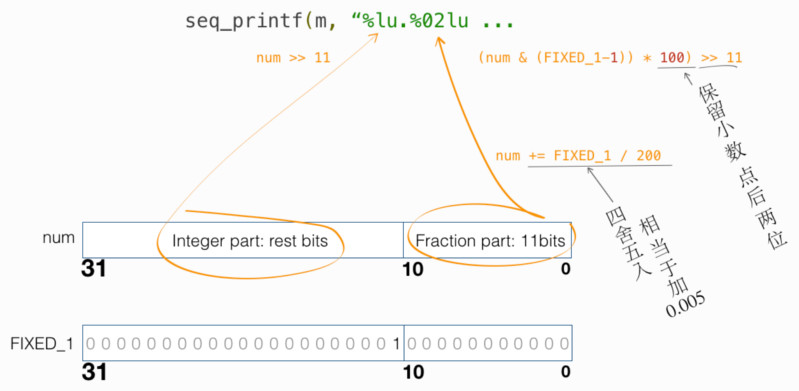
背后的代码为 loadavg_proc_show()。其中逻辑在于：

1. 如何用 int 类型来编码 一定精度的小数 ？
2. 如何 printf 如上编码的小数？
3. 若要保留 n 位，如何四舍五入？

以上弎问题答案图示如下：

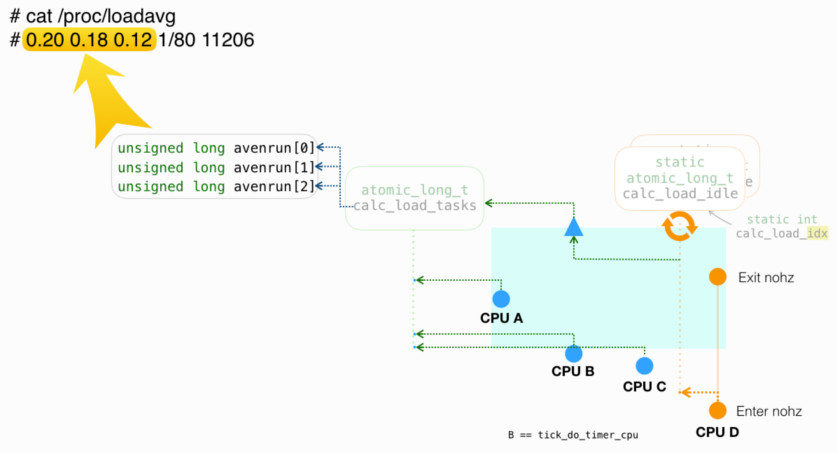
统计量 avenrun[3]

/proc/loadavg 内容来自全局统计量 avenrun[3]，后者在函数 calc_global_load()，由 全局变量 calc_load_tasks 计算而来，如下图所示：

若 kernel 允许进行浮点操作，则其计算公式为：

/* 每 5 秒采样一次，1 分钟内的均值 */
float avenrun_f[0] = avenrun_f[0] * e^(-5/60) + calc_load_tasks * (1.0 - e^(-5/60);

/* 每 5 秒采样一次，5 分钟内的均值 */
float avenrun_f[1] = avenrun_f[1] * e^(-5/300) + calc_load_tasks * (1.0 - e^(-5/300);

/* 每 5 秒采样一次，15 分钟内的均值 */
float avenrun_f[2] = avenrun_f[2] * e^(-5/900) + calc_load_tasks * (1.0 - e^(-5/900);

然而，为支持无 FPU 硬件，同时也避免污染 FPU context，kernel 采用定点模拟浮点，如下表：

对应代码位于函数 calc_load()。留意当 “active >= load”，会进行 “ceil” 形式的向上进位。

任务数（calc_load_tasks）来衡量负载

全局变量 calc_load_tasks 记录了处于 ‘R’ 和 ‘DI’ 状态的任务数：

• Commit: 每隔 5s，各个 CPU 以 delta 形式，上报给 calc_load_tasks
  • 每隔 5s 是通过在 tick 中比较 jiffies 和 rq->calc_load_update 做到的
  • 对应代码：calc_global_load_tick()
  • 下图例中，对应蓝色圆点
• Sampling: 每隔 5s，索引为 tick_do_timer_cpu 的 CPU 将 calc_load_tasks 累计入 avenrun[3]
  • 每隔 5s 是通过在 tick 中比较 jiffies 和 calc_load_update 做到的
  • 对应代码：calc_global_load()
  • 下图例中，对应蓝色三角

如下图所示：

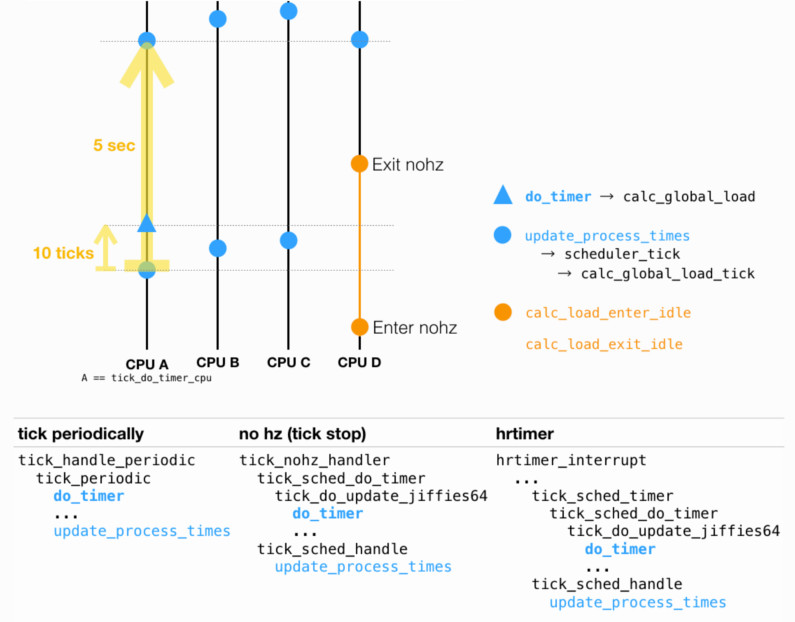
进一步说明图中 “tick 处理”，分成俩维度：1) periodic tick 和 NOHZ；2）是否使用高精度 timer。其中 tickless 意味着 CPU idle 或仅有一个任务。

对其中细节感兴趣的，大家可以出门左转阅读蜗窝的时间子系统系列。特别是「periodic tick」、「Tick Device layer综述」和「tick broadcast framework」

拾遗：针对 nohz 的补丁

上文提到了间隔 5s 的 tick 中，更新 calc_load_tasks，并累计入 avenrun[3]。然而，处于 nohz 模式时，tick 不定期到达（dynamic tick），分为俩情形：

• Patch commit：当前 CPU 进入 nohz，将其原本要提交的 delta，存入 calc_load_idle[idx]
  • calc_load_idle[2] 是个 “double buffer”：“front buffer” 由 calc_load_idx 所指出。
  • 在 calc_global_load() → calc_load_fold_idle() 中，“front buffer” 被消费（“front buffer” 清 0）
  • 在 calc_global_load() → calc_global_nohz() 中，swap “front/back buffer”。
  • 对应代码：calc_load_enter_idle()
  • 退出 nohz 对应代码：calc_load_exit_idle() —— 主要是更新 rq->calc_load_update：取决于是否在 “10 ticks 的 sampling window” 内，或为 calc_load_update + 5s，或就是全局时间戳 calc_load_update。
• Patch sampling：当全部 CPU 进入 nohz，采样间隔可能 >5s，即可能错过多个采样周期，需要一次性补回来：

/* code snippet in calc_global_nohz() */
sample_window = READ_ONCE(calc_load_update);
if (!time_before(jiffies, sample_window + 10)) {
	/*
	 * Catch-up, fold however many we are behind still
	 */
	delta = jiffies - sample_window - 10;
	n = 1 + (delta / LOAD_FREQ);

	active = atomic_long_read(&calc_load_tasks);
	active = active > 0 ? active * FIXED_1 : 0;

	avenrun[0] = calc_load_n(avenrun[0], EXP_1, active, n);
	avenrun[1] = calc_load_n(avenrun[1], EXP_5, active, n);
	avenrun[2] = calc_load_n(avenrun[2], EXP_15, active, n);

	WRITE_ONCE(calc_load_update, sample_window + n * LOAD_FREQ);
}

留意补偿后，calc_load_update 须是个未来的时间戳，故而 n 计算中还有 “+ 1”。

在具体的“采样累计”算法上，要考虑 missing 的采样周期，这就是函数 calc_load_n()：

/*
 * a1 = a0 * e + a * (1 - e)
 *
 * a2 = a1 * e + a * (1 - e)
 *    = (a0 * e + a * (1 - e)) * e + a * (1 - e)
 *    = a0 * e^2 + a * (1 - e) * (1 + e)
 *
 * a3 = a2 * e + a * (1 - e)
 *    = (a0 * e^2 + a * (1 - e) * (1 + e)) * e + a * (1 - e)
 *    = a0 * e^3 + a * (1 - e) * (1 + e + e^2)
 *
 *  ...
 *
 * an = a0 * e^n + a * (1 - e) * (1 + e + ... + e^n-1) [1]
 *    = a0 * e^n + a * (1 - e) * (1 - e^n)/(1 - e)
 *    = a0 * e^n + a * (1 - e^n)
 *
 * [1] application of the geometric series:
 *
 *              n         1 - x^(n+1)
 *     S_n := \Sum x^i = -------------
 *             i=0          1 - x
 */	
static unsigned long
calc_load_n(unsigned long load, unsigned long exp,
            unsigned long active, unsigned int n)
{
	return calc_load(load, fixed_power_int(exp, n), active);
}

函数头这个拉风的注释中，a0 为旧值，推导了补偿到 a1（a0 之后的一个 5s 周期），补偿到 a2（a0 之后两个周期），一直到 an（a0 之后 n 个周期）。

留意 an 推导中，1 + e + ... + e^n-1 = 1 * (1 - e^n) / (1 - e)，应用了等比数列求和公式（共 n 项，比值为 e，第一项为 e^0 == 1）。

最后，fixed_power_int() 是个浮点数 “整数次方” 的模拟：

/* 计算 x^n 的值 */
static unsigned long
fixed_power_int(unsigned long x, unsigned int n)
{
	unsigned long result = FIXED_1;

	if (n) {
		for (;;) {
			if (n & 1) {
				/* 
				 * 模拟浮点乘法，例如：
				 *  result = 0.21 * FIXED_1
				 *  x = 0.92 * FIXED_1
				 *  result * x = 0.21 * 0.92 * FIXED_1
				 *             = 0.21 FIXED_1 * 0.92 * FIXED_1 / FIXED_1
				 */
				result *= x;
				result += FIXED_1 / 2; /* 四舍五入 */
				result /= FIXED_1;
			}
			n >>= 1;
			if (!n)
				break;
			x *= x;
			x += FIXED_1 / 2; /* 四舍五入 */
			x /= FIXED_1;
		}
	}

	return result;
}

留意循环中，x^n == x^(n0 * 2^0 + n1 * 2^1 + ... nk * 2^k)，其中 nk 取值 0 或 1 —— 即把 n 做二进制展开 —— 对于 “nk == 0” 项目，求和中跳过不累加，这就是“if (n & 1)”处的分支。